
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)
\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)

a,(x+2y)3 =x3+3.x2.2y+3.x.(2y)2+(2y)3
= x3+6x2y+12xy2+8y3
b, phần b tương tự dấu thay đổi một tí
c, (5x+1)(5x+1)= (5x+1)2
=25x2+10x+1

a) Khai triển biểu thức \({\left( {5{\rm{x}} - y} \right)^2}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
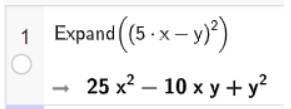
Vậy \({\left( {5{\rm{x}} - y} \right)^2} = 25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2}\)
b) Khai triển biểu thức: \({\left( {\frac{1}{3}x + 2y} \right)^3}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
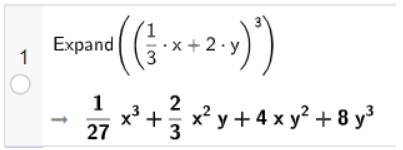
Vậy \({\left( {\frac{1}{3}x + 2y} \right)^3} = \frac{1}{{27}}{x^3} + \frac{2}{3}{x^2}y + 4{\rm{x}}{y^2} + 8{y^3}\)

1.
a) \({\left( {x + 3} \right)^3} = {x^3} + 3.{x^2}.3 + 3.x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)
b) \({\left( {x + 2y} \right)^3} = {x^3} + 3.{x^2}.2y + 3.x.{\left( {2y} \right)^2} + {\left( {3y} \right)^3} = {x^3} + 6{x^2}y + 12x{y^2} + 27{y^3}\)
2.
\(\begin{array}{l}{\left( {2x + y} \right)^3} - 8{x^3} - {y^3} = {\left( {2x} \right)^3} + 3.{\left( {2x} \right)^2}.y + 3.2x.{y^2} + {y^3} - 8{x^3} - {y^3}\\ = 8{x^3} + 12{x^2}y + 6x{y^2} + {y^3} - 8{x^3} - {y^3}\\ = \left( {8{x^3} - 8{x^3}} \right) + 12{x^2}y + 6x{y^2} + \left( {{y^3} - {y^3}} \right)\\ = 12{x^2}y + 6x{y^2}\end{array}\)
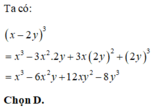
Khai triển hằng đẳng thức :
\(\left(x-2y\right)^3=x^3-6x^2y+12xy^2-8y^3\)