
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)

Câu 3:
Gọi số học sinh lớp 9A là \(x\)(học sinh) (điều kiện: \(x\inℕ^∗;x< 80\)).
Số học sinh lớp 9B là \(80-x\)(học sinh).
Tổng số quyển sách lớp 9A góp được trong đợt góp sách ủng hộ là \(2x\)(quyển sách).
Tổng số quyển sách lớp 9B góp được trong đợt góp sách ủng hộ là \(3\left(80-x\right)\)(quyển sách).
Vì lớp 9A và 9B góp được 198 quyển nên ta có phương trình:
\(2x+3\left(80-x\right)=198\).
\(\Leftrightarrow2x+240-3x=198\).
\(\Leftrightarrow2x-3x=198-240\).
\(\Leftrightarrow-x=-42\).
\(\Leftrightarrow x=42\)(thỏa mãn điều kiện).
Số học sinh lớp 9B là \(80-42=38\).
Vậy lớp 9A có 42 học sinh, lớp 9B có 38 học sinh.

dap an ra \(\left(x-3+\sqrt{6}\right).\left(x-3-\sqrt{6}\right)\)

4: \(D=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(A=\left(x^2-6x+9\right)-7=\left(x-3\right)^2-7\ge7\\ A_{min}=7\Leftrightarrow x=3\\ B=\left(9x^2+6x+1\right)-4=\left(3x+1\right)^2-4\ge-4\\ B_{min}=-4\Leftrightarrow x=-\dfrac{1}{3}\\ C=\left(x^2-2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\\ C_{min}=-\dfrac{9}{4}\Leftrightarrow x=\dfrac{5}{2}\\ D=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ D_{min}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(E=3\left(x^2+2\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\\ E_{min}=-\dfrac{4}{3}\Leftrightarrow x=-\dfrac{1}{3}\\ F=x^2-2x+1+x^2-4x+4+2021\\ F=2\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{4031}{2}=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{4031}{2}\ge\dfrac{4031}{2}\\ F_{min}=\dfrac{4031}{2}\Leftrightarrow x=\dfrac{3}{2}\)




 Giúp mình bài này với cô giáo mình giao trên mạng cô bảo cô bảo cho hướng dẫn nhưng lại k cho
Giúp mình bài này với cô giáo mình giao trên mạng cô bảo cô bảo cho hướng dẫn nhưng lại k cho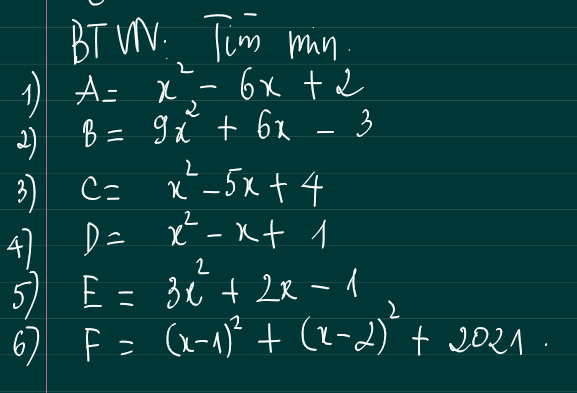

Bài 1:
a)
\(\dfrac{5x-2}{3}=\dfrac{5-3x}{2}\\ 2\left(5x-2\right)=3\left(5-3x\right)\\ 10x-4=15-9x\\ 19x=19\\ x=1\)
b)
\(\dfrac{10x+3}{12}=1+\dfrac{6+8x}{9}\\ \dfrac{10x+3}{3.4}=\dfrac{15+8x}{3.3}\\3\left(10x+3\right)=4\left(15+8x\right)\\ 30x+9=60+32x\\ 2x=-51\\ x=-\dfrac{51}{2}. \)
c) \(\dfrac{x^2-10x-29}{1971}-1+\dfrac{x^2-10x-27}{1973}-1=\dfrac{x^2-10x-1971}{29}+\dfrac{x^2-10x-1973}{27}\\ \dfrac{x^2-10x-2000}{1971}+\dfrac{x^2-10x-2000}{1973}=\dfrac{x^2-10x-2000}{29}+\dfrac{x^2-10x-2000}{27}\\\left(x^2-10x-2000\right).\left(\dfrac{1}{1971}+\dfrac{1}{1973}-\dfrac{1}{29}-\dfrac{1}{27}\right)=0\\ x^2-10x-2000=0\\ \left[{}\begin{matrix}x=50\\x=-40\end{matrix}\right.\)
d) \(\dfrac{5x-2}{2-2x}+\dfrac{2x-1}{2}=1-\dfrac{x^2+x-3}{1-x}\\ \dfrac{5x-2}{2-2x}+\dfrac{\left(2x-1\right)\left(1-x\right)}{2\left(1-x\right)}=\dfrac{1-x-x^2-x+3}{1-x}\\ \dfrac{5x-2-2x^2+3x-1}{2-2x}=\dfrac{-x^2-2x+4}{1-x}\\ -2x^2+8x-3=-2x^2-4x+8\\12x=11\\ x=\dfrac{11}{12}.\)
e)
\(\dfrac{3}{4\left(x-5\right)}+\dfrac{15}{50-2x^2}=-\dfrac{7}{6\left(x+5\right)}\left(đk:x\ne\pm5\right)\\ \dfrac{3\left(x+5\right)}{4\left(x-5\right)\left(x+5\right)}+\dfrac{15.2}{2\left(5-x\right)\left(5+x\right)}=\dfrac{-7\left(x-5\right)}{6\left(x+5\right)\left(x-5\right)}\\ 9\left(x+5\right)-15.2.6=-14\left(x-5\right)\\ 9x+45-180=-14x+70\\ 23x=205\\ x=\dfrac{205}{23}\left(tmđk\right).\)