Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vd : \(x^2+6x+10\)
Ta có : 10 không căn được
Mà : \(x^2+2.x.3+3^2\)
Nhưng 32 chỉ là 9 nên ta cộng thêm 1 ở vế sau
\(\left(x^2+2.x.3+3^2\right)+1\)
\(\left(x+3\right)^2+1\)
Dư 1 ở ngoài :
Vì \(\left(x+3\right)^2\ge0\)
=> \(\left(x+3\right)^2+1\ge1\)
=> GTNN là 1
Khi ( x + 3 ) = 0
x = -3
Khi
Giải
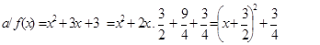
Ta có 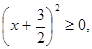 nên
nên 
Vậy: f(x) đạt GTNN bằng  khi
khi 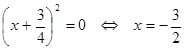
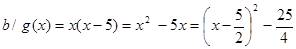
Ta có  nên
nên 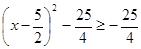
Vậy: g(x) đạt GTNN bằng  khi
khi 

\(2\left(x-1\right)^2-4\left(3+x^2\right)+2x\left(x-5\right)\)
\(2.x^2-2.x.1+1^2-12-4x^2+2x^2-10x\)
\(2x^2-2x+1-12-4x^2+2x^2-10x\)
\(-12x-11\)

1,2,3,4 không tính được.
`5)(2x-1/2)^2`
`=(2x)^2-2+(1/2)^2`
`=4x^2-2+1/4`
`6)(x+1/4)^2`
`=x^2+1/2x+1/16`

Q = (1 - 2x)(x - 3)
= x - 3 - 2x2 + 6x
= - 2x2 + 5x - 3
= \(-2\left(x^2-\frac{5}{2}x+3\right)=-2\left(x^2-2.\frac{5}{4}.x+\frac{25}{16}+\frac{23}{16}\right)=-2\left(x-\frac{5}{4}\right)^2-\frac{23}{8}\le-\frac{23}{8}\)
Dấu "=" xảy ra <=> x - 5/4 = 0
=> x = 1,25
Vậy Max Q = -23/8 <=> x = 1,25
Q = ( 1 - 2x )( x - 3 )
= x - 3 - 2x2 + 6x
= -2x2 + 7x - 3
= -2( x2 - 7/2x + 49/16 ) + 25/8
= -2( x - 7/4 )2 + 25/8 ≤ 25/8 ∀ x
Đẳng thức xảy ra <=> x - 7/4 = 0 => x = 7/4
=> MaxQ = 25/8 <=> x = 7/4

a) \(x^2-4x+7\)
\(\Leftrightarrow x^2-4x+4+3\)
\(\Leftrightarrow\left(x-2\right)^2+3\ge3\)với mọi x
Dấu "=" xảy ra khi x-2=0 <=> x=2

bài đó có dạng
ax4+bx3+cx2+dx+e=0 (Với b=d hoặc b=-d)
Cách làm có nhìu cách tui chỉ rành một cách nên tui chỉ
Với b=d thì đặt t=x2+1
Với b=-d thì đặt t=x2-1
tự nguyên cứu tiếp đi
ta xét thấy đây là phương trình đối xứng vì hệ số của các số hạng cách đều số hạng đầu và số hạng cuối bằng nhau (ví dụ 3x4 và 3 có cùng hệ số là 3, -13x3 và -13x có cùng hệ số là -13....)
cụ thể đây là phương trình đối xứng bậc chẵn (số hạng đàu có bậc chẵn là 4)
giải như sau
ta nhẩm thấy 0 không phải là nghiệm của phương trình nên chia cả hai vế cho x2 ta có
3x2-13x+16-13/x + 3/x2 =0
<=>(3x^2 + 3/x^2) - (13x + 13/x) +16 =0
<=>3(x^2 + 1/x^2) - 13(x+1/x)=0
đặt x+1/x = a thì x^2+1/x^2=a^2 - 2 (cái này bạn dùng hằng đẳng thức (a+b)^2 để suy ra nhé)
thay vào ta được
3a - 13(a^2 - 2) +16 = 0
3a - 13a^2 + 26 =0
đến đây bạn giải a bằng cách đưa về phương trình tích rồi tìm x là xong

a-b=7
(a-b)2=a2+b2-2ab=49
a2+b2+4ab-2ab=49+32=81
(a+b)2=81
a+b=9 hoặc a+b=(-9)
Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)