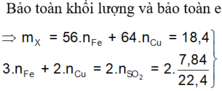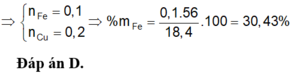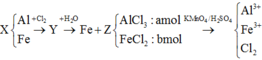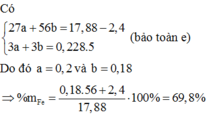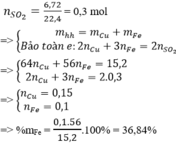Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$a)$
Đặt $n_{Al}=x(mol);n_{Fe}=y(mol)$
$\to 27x+56y=13,75(1)$
Bảo toàn e: $1,5x+y=n_{H_2}=\dfrac{11,2}{22,4}=0,5(2)$
Từ $(1)(2)\to x=0,25(mol);y=0,125(mol)$
$\to \%m_{Al}=\dfrac{0,25.27}{13,75}.100\%\approx 49,09\%$
$\to \%m_{Fe}=100-49,09=50,91\%$
$b)$
Bảo toàn H: $n_{HCl}=2n_{H_2}=1(mol)$
$\to a=\dfrac{1.36,5.120\%}{18,25\%}=240(g)$
$c)$
Bảo toàn Al,Fe: $n_{AlCl_3}=0,25(mol);n_{FeCl_2}=0,125(mol)$
$m_{dd_{HCl(p/ứ)}}=\dfrac{1.36,5}{18,25\%}=200(g)$
Ta có $m_{dd\, sau}=13,75+200-0,5.2=212,75(g)$
$\to \begin{cases} C\%_{AlCl_3}=\dfrac{0,25.133,5}{212,75}.100\%=15,69\%\\ C\%_{FeCl_2}=\dfrac{0,125.127}{212,75}.100\%=7,46\% \end{cases}$

Đáp án D.
Gọi nCu = y, nFe = x mol

Áp dụng định luật bảo toàn e ta có: 3x+2y = 0,7 (1)
Khối lượng hai kim loại = 1,84 g: 56x+64y = 184 (2).
Giải 1,2 ta có: x = 0,1, y = 0,2 (mol)
% m F e = 0 , 1 . 56 18 , 4 . 100 % = 30 , 43 %

Đáp án B
Fe là kim loại yếu hơn Al =>Al phản ứng trước, Fe phản ứng sau => 2,4 gam kim loại chính là Fe dư
Gọi số mol các chất là Al: a mol; Fe (pứ): b mol
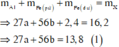
KMnO4 là chất oxi hoá mạnh, trong môi trường axit sẽ oxi hoá Fe + 2 lên Fe + 3 , Cl - 1 lên Cl 2 0 và bản thân Mn + 7 bị khử xuống Mn + 2
Như vậy, khi xét cả quá trình thì chỉ có Al, Fe và KMnO4 thay đổi số oxi hoá:
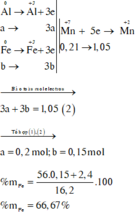

a)
Gọi \(\left\{{}\begin{matrix}n_{Fe}=a\left(mol\right)\\n_{Mg}=b\left(mol\right)\end{matrix}\right.\)
=> 56a + 24b = 18,4 (1)
PTHH: Fe + 2HCl --> FeCl2 + H2
a-->2a------>a------>a
Mg + 2HCl --> MgCl2 + H2
b--->2b------->b------>b
=> \(a+b=\dfrac{11,2}{22,4}=0,5\) (2)
(1)(2) => a = 0,2 (mol); b = 0,3 (mol)
\(\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,2.56}{18,4}.100\%=60,87\%\\\%m_{Mg}=\dfrac{0,3.24}{18,4}.100\%=39,13\%\end{matrix}\right.\)
b) \(n_{HCl\left(pư\right)}=2a+2b=1\left(mol\right)\)
=> \(n_{HCl\left(tt\right)}=\dfrac{1.125}{100}=1,25\left(mol\right)\)
=> mHCl(tt) = 1,25.36,5 = 45,625 (g)
=> \(a=\dfrac{45,625.100}{18,25}=250\left(g\right)\)
c)
mdd sau pư = 18,4 + 250 - 0,5.2 = 267,4 (g)
\(C\%_{FeCl_2}=\dfrac{0,2.127}{267,4}.100\%=9,5\%\)
\(C\%_{MgCl_2}=\dfrac{0,3.95}{267,4}.100\%=10,66\%\)