
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



c: Ta có: \(\dfrac{\sqrt{x}-10}{\sqrt{x}+2}\ge-2\)
\(\Leftrightarrow\sqrt{x}-10+2\left(\sqrt{x}+2\right)\ge0\)
\(\Leftrightarrow3\sqrt{x}\ge6\)
hay \(x\ge4\)

Bài 9:
c) Ta có: \(P=\dfrac{a\sqrt{a}-1}{\sqrt{a}-1}\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}-1}\)
\(=a+\sqrt{a}+1\)
d) Ta có: \(Q=\dfrac{a\sqrt{a}+1}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=a-\sqrt{a}+1\)

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)EB tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>BF\(\perp\)FC tại F
=>BF\(\perp\)AC tại F
Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp đường tròn đường kính AH
tâm K là trung điểm của AH
b:
Ta có: OE=OC
=>ΔOEC cân tại O
=>\(\widehat{OEC}=\widehat{OCE}\)
Ta có: ΔKHE cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
\(\widehat{KEO}=\widehat{KEC}+\widehat{OEC}\)
\(=\widehat{OCE}+\widehat{KHE}\)
\(=\widehat{ECB}+\widehat{DHC}=90^0\)
=>KE là tiếp tuyến của (O)
Xét ΔKEO và ΔKFO có
KE=KF
EO=FO
KO chung
Do đó: ΔKEO=ΔKFO
=>\(\widehat{KEO}=\widehat{KFO}=90^0\)
Ta có: \(\widehat{KEO}=\widehat{KFO}=\widehat{KDO}=90^0\)
=>K,E,O,F,D cùng thuộc đường tròn đường kính KO(ĐPCM)

a: Ta có: \(\sqrt{75}-\sqrt{5\dfrac{1}{3}}+\dfrac{9}{2}\sqrt{2\dfrac{2}{3}}+2\sqrt{27}\)
\(=5\sqrt{3}+\dfrac{4}{3}\sqrt{3}+3\sqrt{6}+6\sqrt{3}\)
\(=\dfrac{37}{3}\sqrt{3}+3\sqrt{6}\)
c: Ta có: \(\left(\sqrt{12}+2\sqrt{27}\right)\cdot\dfrac{\sqrt{3}}{2}-\sqrt{150}\)
\(=\left(2\sqrt{3}+6\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=12-5\sqrt{6}\)

c: Thay P=-4 vào P, ta được:
\(-\sqrt{x}=-4x-4\sqrt{x}-4\)
\(\Leftrightarrow4x+3\sqrt{x}+4=0\)


1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)


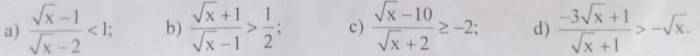 giải câu c và d hộ mik vs
giải câu c và d hộ mik vs 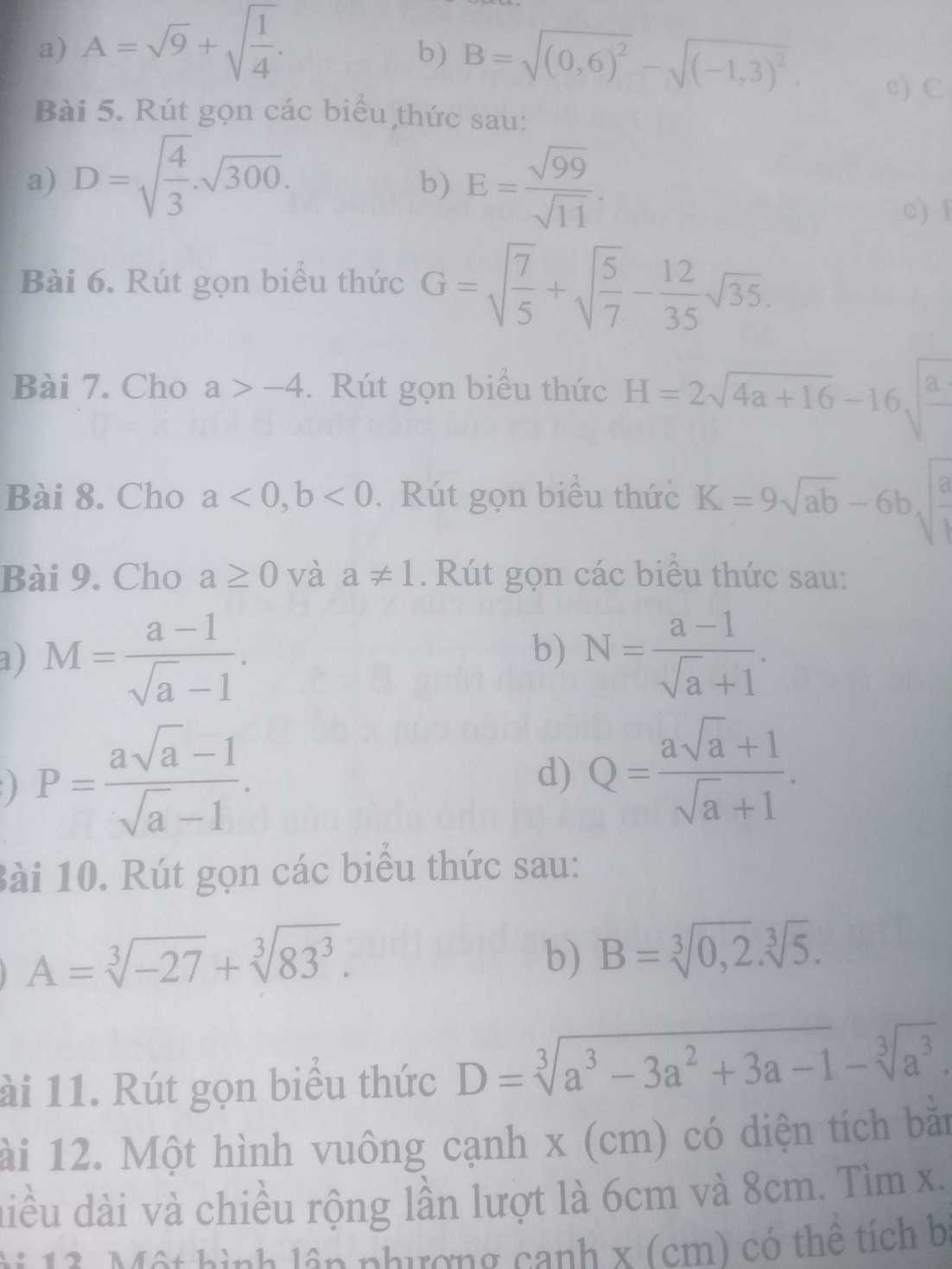



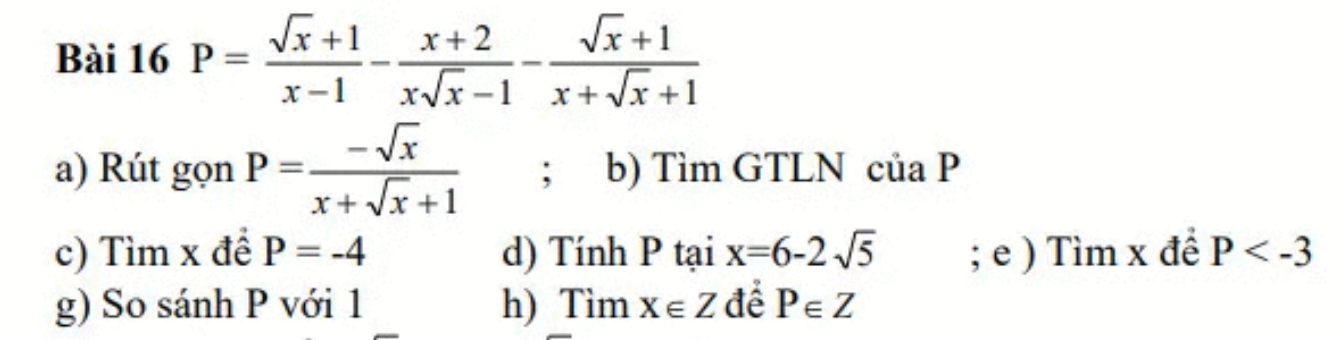


c) \(P=\frac{5}{x}+\frac{6}{y}+\frac{128}{6x+5y}=\frac{6x+5y}{xy}+\frac{128}{6x+5y}\ge2\sqrt{\frac{6x+5y}{xy}.\frac{128}{6x+5y}}=16\)
Dấu \(=\)khi \(\hept{\begin{cases}xy=2\\\left(6x+5y\right)^2=256\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1,y=2\\x=\frac{5}{3},y=\frac{6}{5}\end{cases}}\).
d) \(\frac{a^2}{b-1}+\frac{b^2}{c-1}+\frac{c^2}{a-1}\ge\frac{\left(a+b+c\right)^2}{a+b+c-3}=\frac{t^2}{t-3}=P\)
(với \(t=a+b+c>3\))
\(P\left(t-3\right)=t^2\Leftrightarrow t^2-Pt+3P=0\)(1)
Để phương trình (1) có nghiệm thì:
\(\Delta=P^2-12P\ge0\Leftrightarrow\orbr{\begin{cases}P\ge12\\P\le0\end{cases}}\Rightarrow P\ge12\)(do \(t>3\)nên \(P>0\))
Ta có đpcm.