
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt

a: \(B=\dfrac{x+\sqrt{x}-1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: \(B-\dfrac{1}{3}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}+1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\)
=>B<1/3

c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)

Bài 9:
c) Ta có: \(P=\dfrac{a\sqrt{a}-1}{\sqrt{a}-1}\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}-1}\)
\(=a+\sqrt{a}+1\)
d) Ta có: \(Q=\dfrac{a\sqrt{a}+1}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=a-\sqrt{a}+1\)



\(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\left(dk:x\ge0,x\ne4\right)\\ =\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\\ =\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}\\ =\dfrac{x+2\sqrt{x}}{x-4}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để \(A>1\) thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}>1\Leftrightarrow\dfrac{\sqrt{x}-\sqrt{x}+2}{\sqrt{x}-2}>0\Leftrightarrow2>0\left(LD\right)\)
\(\Leftrightarrow\sqrt{x}-2>0\Leftrightarrow x>4\left(tm\right)\)
Vậy \(x>4\) thì \(A>1\).

\(\left\{{}\begin{matrix}2y-3x=7\\y+4x=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y-12x=28\\3y+12x=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}11y=55\\y+4x=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=5\\5+4x=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=1\end{matrix}\right.\)
Vậy nghiệm hpt: \(\left(x;y\right)=\left(1;5\right)\)
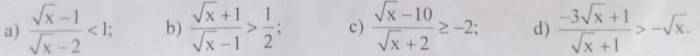 giải câu c và d hộ mik vs
giải câu c và d hộ mik vs 
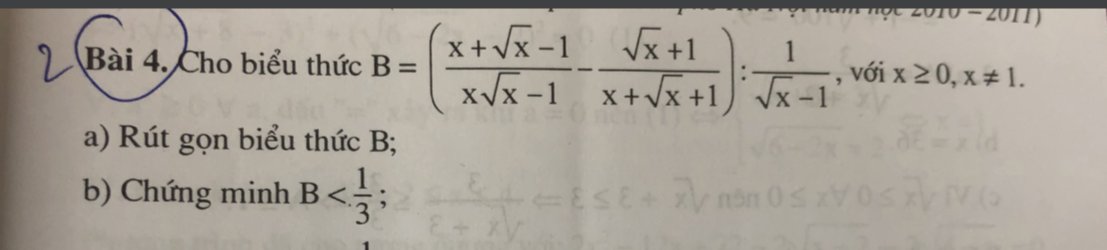
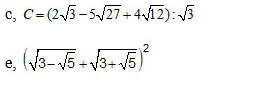
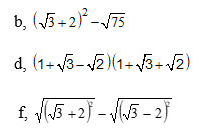 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp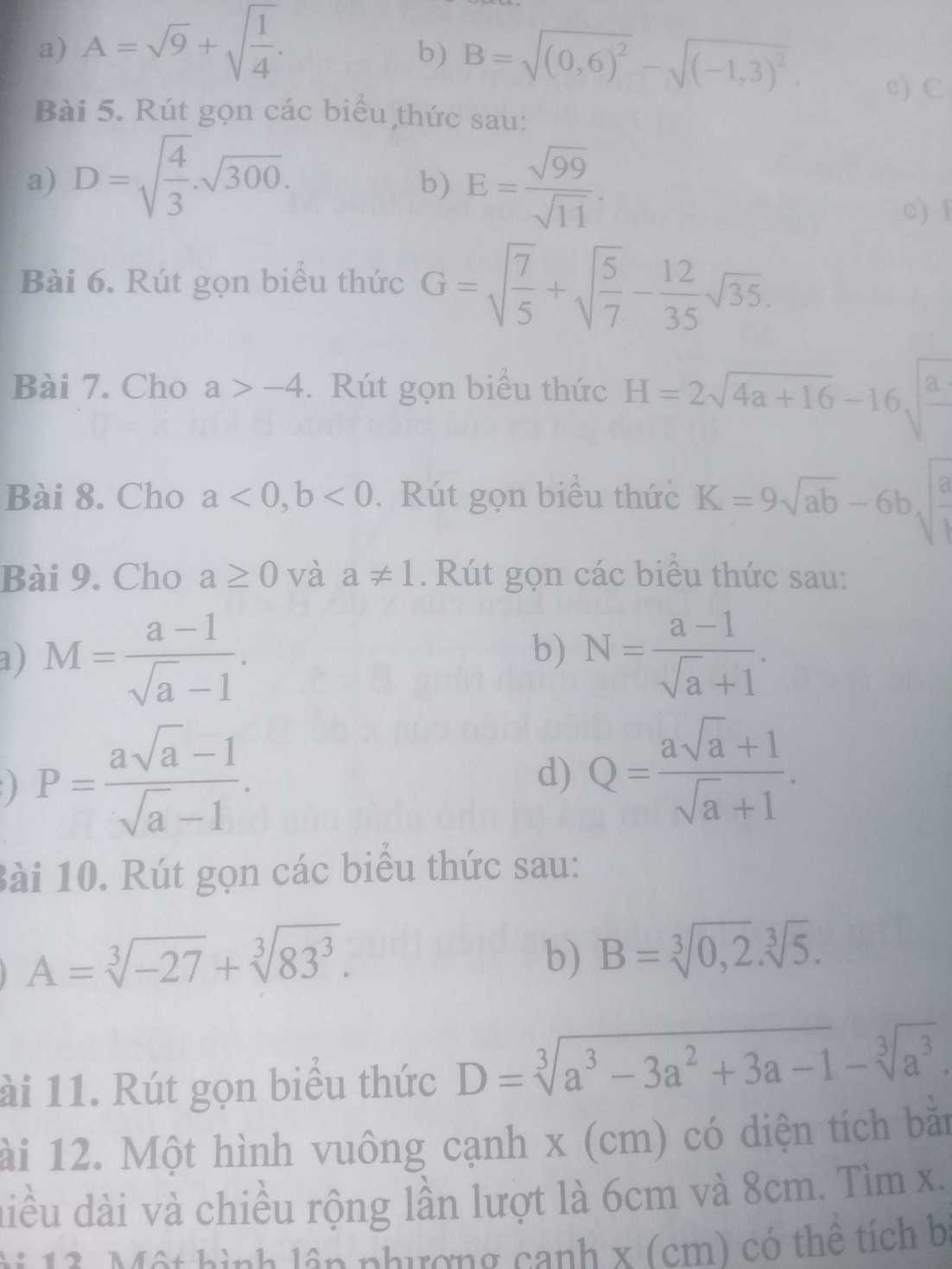


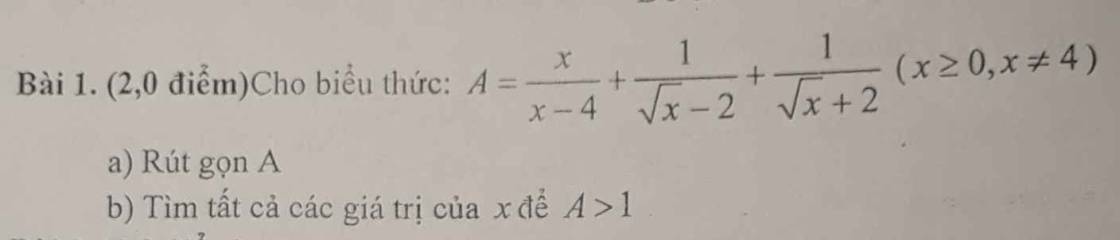

c: Ta có: \(\dfrac{\sqrt{x}-10}{\sqrt{x}+2}\ge-2\)
\(\Leftrightarrow\sqrt{x}-10+2\left(\sqrt{x}+2\right)\ge0\)
\(\Leftrightarrow3\sqrt{x}\ge6\)
hay \(x\ge4\)