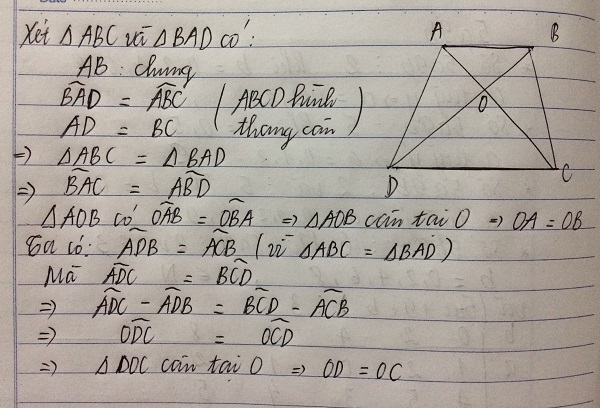Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
∠ (ADC) = ∠ (BCD) (gt)
DC chung
Do đó: ∆ ADC = ∆ BCD (c.g.c) ⇒ ∠ C 1 = ∠ D 1
Trong ∆ OCD ta có: ∠ C 1 = ∠ D 1 ⇒ ∆ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.

Xét tam giác OAD và tam giác OBC ta có:
góc OAD = góc OCB (hai góc so le trong, AB//CD)
AD = BC (Vì hình thang cân có hai cạnh bên bằng nhau)
góc ODA = góc OBC (hai góc so le trong, AB//CD)
=> tam giác OAD = tam giac OBC (g-c-g)
=> OA=OB
chứng minh tương tự ta sẽ được OD=OC

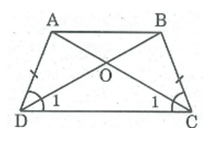
a ) Xét ADC và BCD, ta có:
AD = BC (tính chất hình thang cân)
(ADC) = (BCD) (gt)
DC chung
Do đó: ADC = BCD (c.g.c) ⇒ =
Trong OCD ta có: = ⇒ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
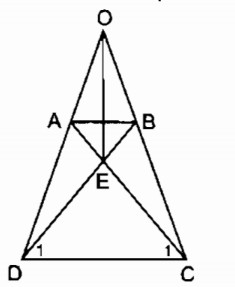
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.

a: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
Suy ra: \(\widehat{CAD}=\widehat{DBC}\)
b: Ta có: ΔADC=ΔBCD
nên \(\widehat{ODC}=\widehat{OCD}\)
hay ΔOCD cân tại O
Suy ra: OC=OD
hay OA=OB

( Hình tự vẽ nha bạn )
giải
Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠ADC= ∠BCD (2 góc tương ứng)
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.