Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.

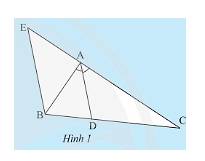
a) Vì \(BE//AD\) nên \(\widehat {EBA} = \widehat {BAD}\) (cặp góc so le trong) (1)
Vì \(BE//AD\) nên \(\widehat {BEA} = \widehat {DAC}\) (cặp góc đồng vị) (2)
Vì \(AD\) là tia phân giác nên \(\widehat {BAD} = \widehat {DAC}\) (tính chất) (3)
Từ (1); (2); (3) suy ra \(\widehat {EBA} = \widehat {AEB}\) (tính chất bắc cầu)
Xét tam giác \(BAE\) có:
\(\widehat {EBA} = \widehat {AEB}\) (chứng minh trên)
Nên tam giác \(BAE\) cân tại \(A\).
b) Vì \(BE//AD\) nên \(\frac{{BD}}{{DC}} = \frac{{AE}}{{AC}}\).
Mà tam giác \(BAE\) cân tại \(A\) nên \(AE = AB \Rightarrow \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (định lí Thales)
Do đó, \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (điều phải chứng minh).
a: AD//BE
=>góc CAD=góc CEB và góc BAD=góc ABE
mà góc CAD=góc BAD
nên góc CEB=góc ABE
=>ΔBAE cân tại A
b: ΔBAE cân tại A
=>AB=AE
=>AB/AC=AE/AC
mà AE/AC=BD/DC(ΔCEB có AD//BE)
nên AB/AC=AE/AC=DB/DC

a , Vì là hình thoi
=> AC vuông góc với DB
=> Góc O = 90 độ , BK // AC
=> BK vuông góc với DB tại B
=> Góc B = 90 độ , CK // DB
=> DK vuông góc với AC tại C
=> Góc C = 90 độ
=> TG là hình chữ nhật ( góc vuông )
b , BK // AC <=> BK // OA
OBKC là hình chữ nhật => BK = OC <=> BK = OC ( OA = OC )
=> TG ABKO là hình bình hành = > OK = AB

a, Do CD//AB, DM//BD nên ta dễ thấy: tam giác DMC đồng dạng với tam giác BCA(g.g)
➞ MCCA=CDAB=AFABMCCA=CDAB=AFAB ( vì ADCF là hình bình hành nên CD=AF) (1)
Ta lại có: FP//AC nên:CPCB=AFABCPCB=AFAB (2)
Từ (1),(2) ta có: CMCA=CPCBCMCA=CPCB
Theo định lí Talet đảo ta có: MP//AB
b, Gọi N, N' là giao điểm của MP,DB với CF
Ta có:CNCF=CMCA=CDABCNCF=CMCA=CDAB ( theo phần a,)
CN′N′F=CDFBCN′N′F=CDFBsuy ra AN′CF=CD(FB+CD)=CDABAN′CF=CD(FB+CD)=CDAB ( vì CD=AF)
Vậy CN=CN' nên N' trùng N
Từ đó ta suy ra: MP,CF,DB đồng quy

a: Xét tứ giác OBKC có
OB//KC
OC//BK
góc BOC=90 độ
Do đó: OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
nên OK=BC
=>OK=AB

AD // CF ---> AFCD là hbh ---> AF = CD
DK // BC ---> DKBC là hbh ---> BK = CD
---> AB-AF = AB-BK hay FB = AK (1)
AM // FB ---> ^MAK = ^PFB (góc đồng vị) (2)
MK // PB ---> ^MKA = ^PBF (góc đồng vị) (3)
(1),(2),(3) ---> 2 t/g MAK và PFB bằng nhau (gcg) ---> MA = PF (4)
Mà AC // PF ---> MA // PF (5)
(4),(5) ---> MAFB là hbh ---> MP // AF ---> MP // AB
b)
Gọi Q là giao điểm của MP và CF, B' là giao điểm của DQ và AB ---> B và B' nằm cùng phía đối với đt CF
CD // FB' ---> 2 t/g QCD và QFB' đồng dạng ---> QC/QF = CD/FB' (5)
QP // FB ---> QC/QF = PC/PB (6)
FB // AC ---> PC/PB = FA/FB = CD/FB (7)
(5),(6),(7) ---> FB' = FB
Mà B và B' nằm cùng phía đối với đt CF nên B' trùng B ---> DB đi qua Q hay nói cách khác MP,CF,DB đồng quy tại Q
chà tìm thấy trên mạng :)

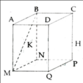
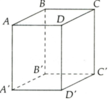
a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').
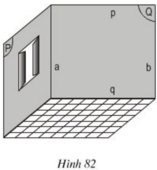
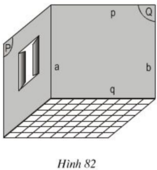

a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.