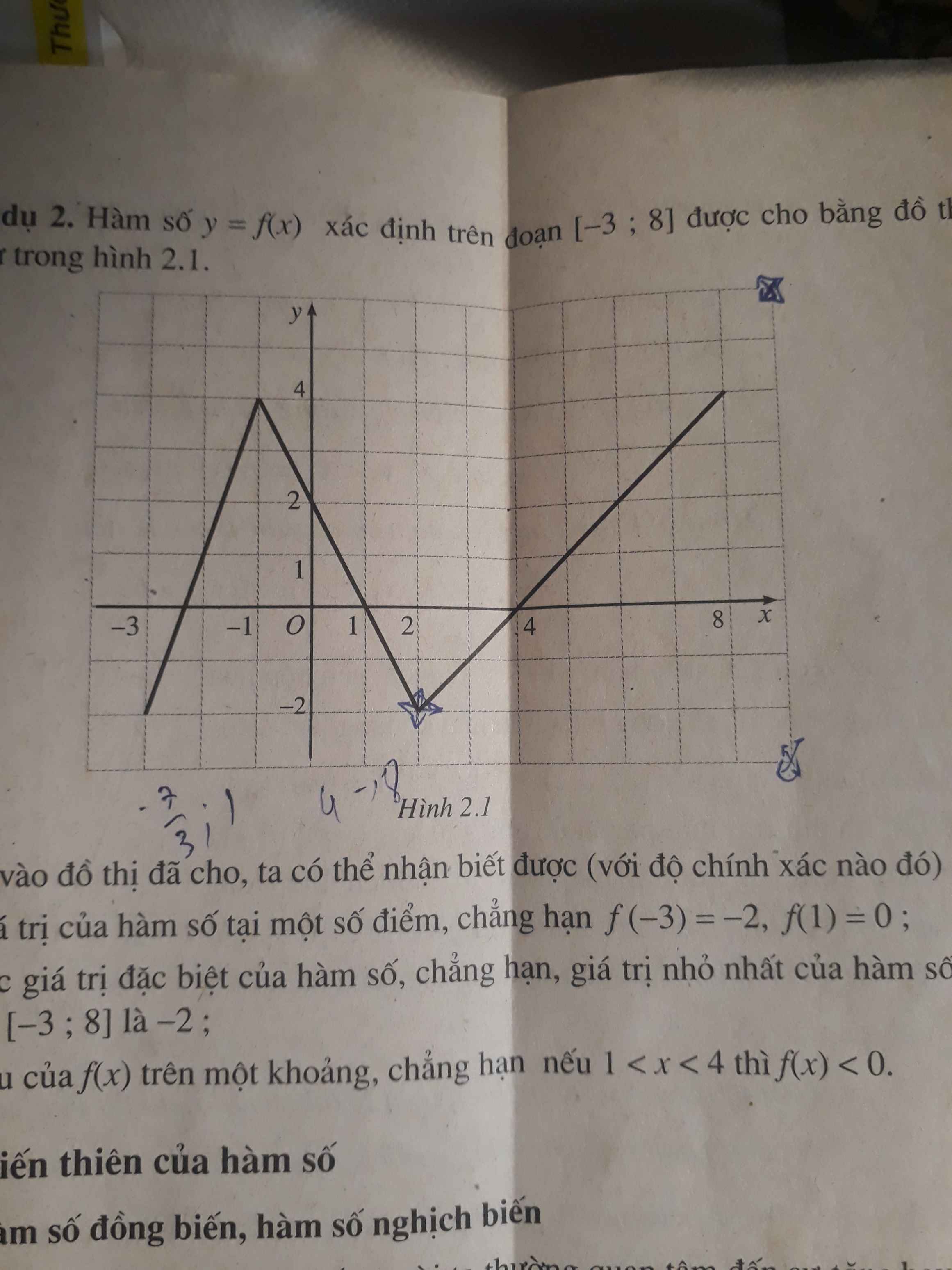Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)

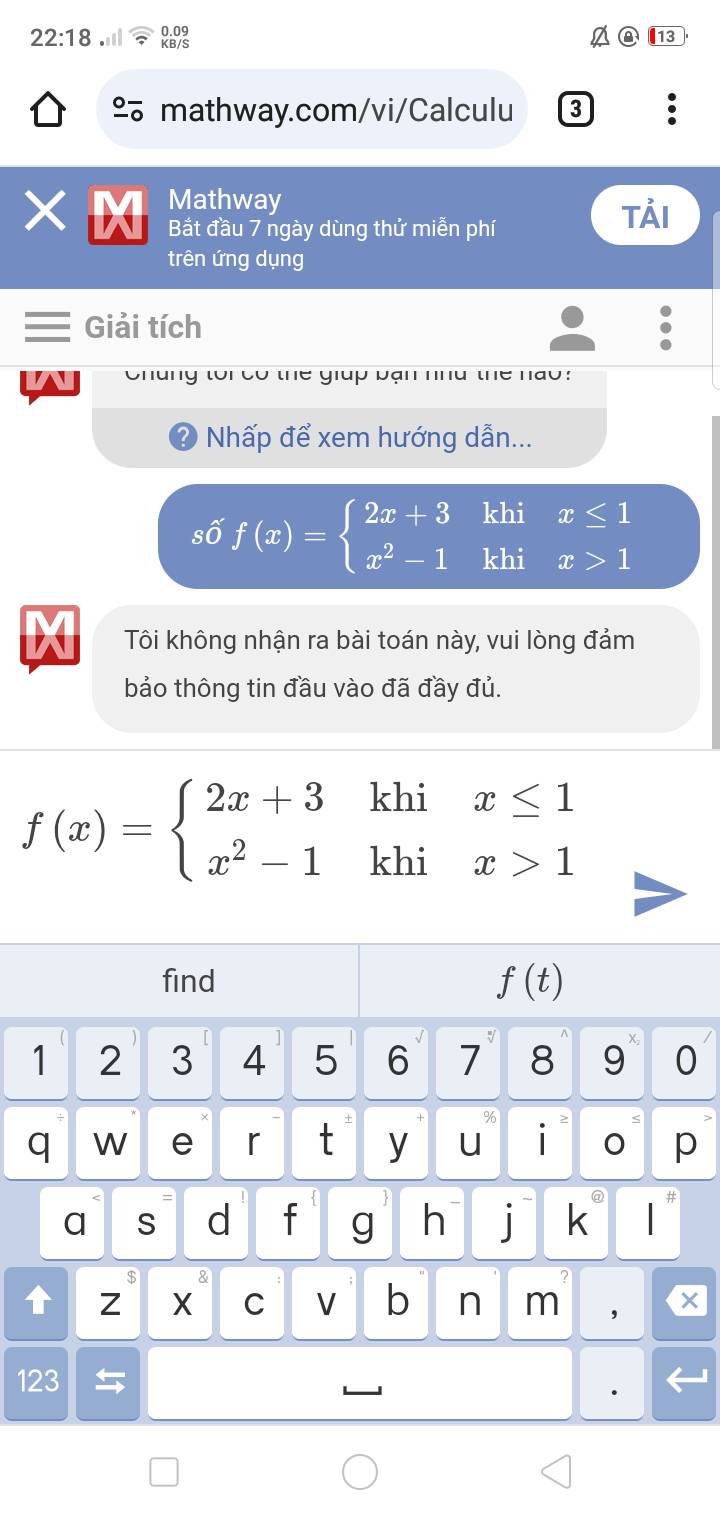
Hàm \(y=f\left(x\right)\) có đồ thị (C):
\(\Rightarrow\) Khi tịnh tiến lên a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x\right)+a\)
Khi tịnh tiến xuống dưới a đơn vị ta được đồ thị hàm \(y=f\left(x\right)-a\)
- Khi tịnh tiến sang phải a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x-a\right)\)
- Khi tịnh tiến sang trái a đơn vị sẽ được đồ thị hàm \(y=f\left(x+a\right)\)
Do đó:
Khi tịnh tiến (P) lên 4 đơn vị ta được đồ thị hàm \(y=4x^2+4\)
Khi tịnh tiến (P) sang phải 2 đơn vị ta được đồ thị hàm: \(y=4\left(x-2\right)^2=4x^2-16x+16\)

a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a-2+c=0\\4a+c+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+c=2\\4a+c=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-6\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\c=0\end{matrix}\right.\)

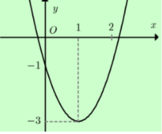
Đồ thị có bề lõm hướng lên trên, loại đáp án C
Đỉnh của parabol là (1; -3) suy ra đán án B thỏa mãn
Chọn B.

Đáp án D
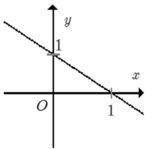
Đồ thị đi xuống từ trái sang phải => hệ số góc a < 0. Loại A, C.
Đồ thị hàm số cắt trục tung tại điểm (0; 1).

Đáp án D
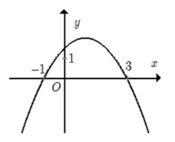
Nhận xét:
Parabol có bề lõm hướng xuống. Loại đáp án A, C.
Parabol cắt trục hoành tại 2 điểm (3; 0) và (−1; 0). Xét các đáp án B và D, đáp án D thỏa mãn.