Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

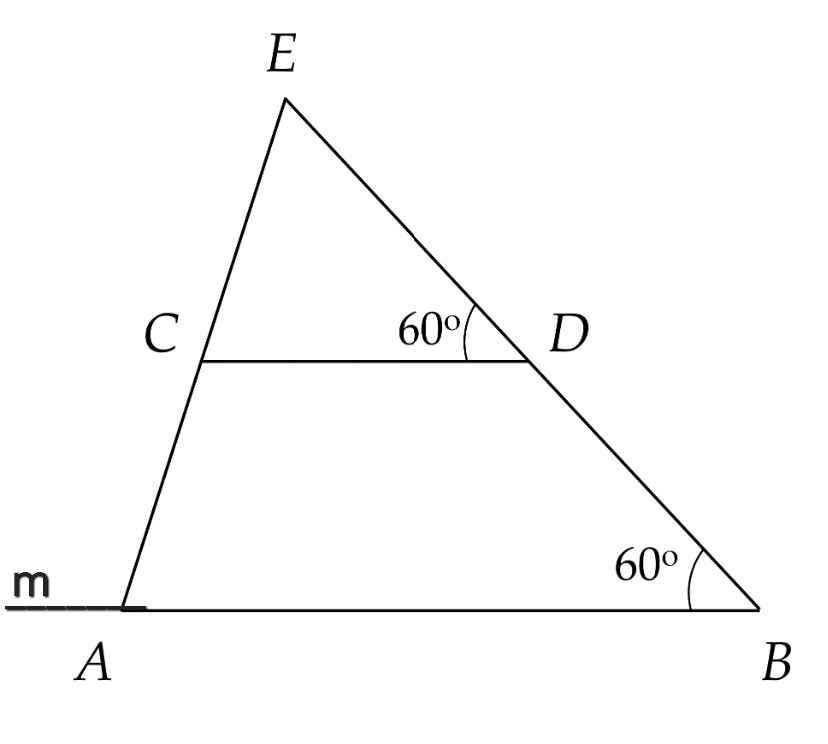
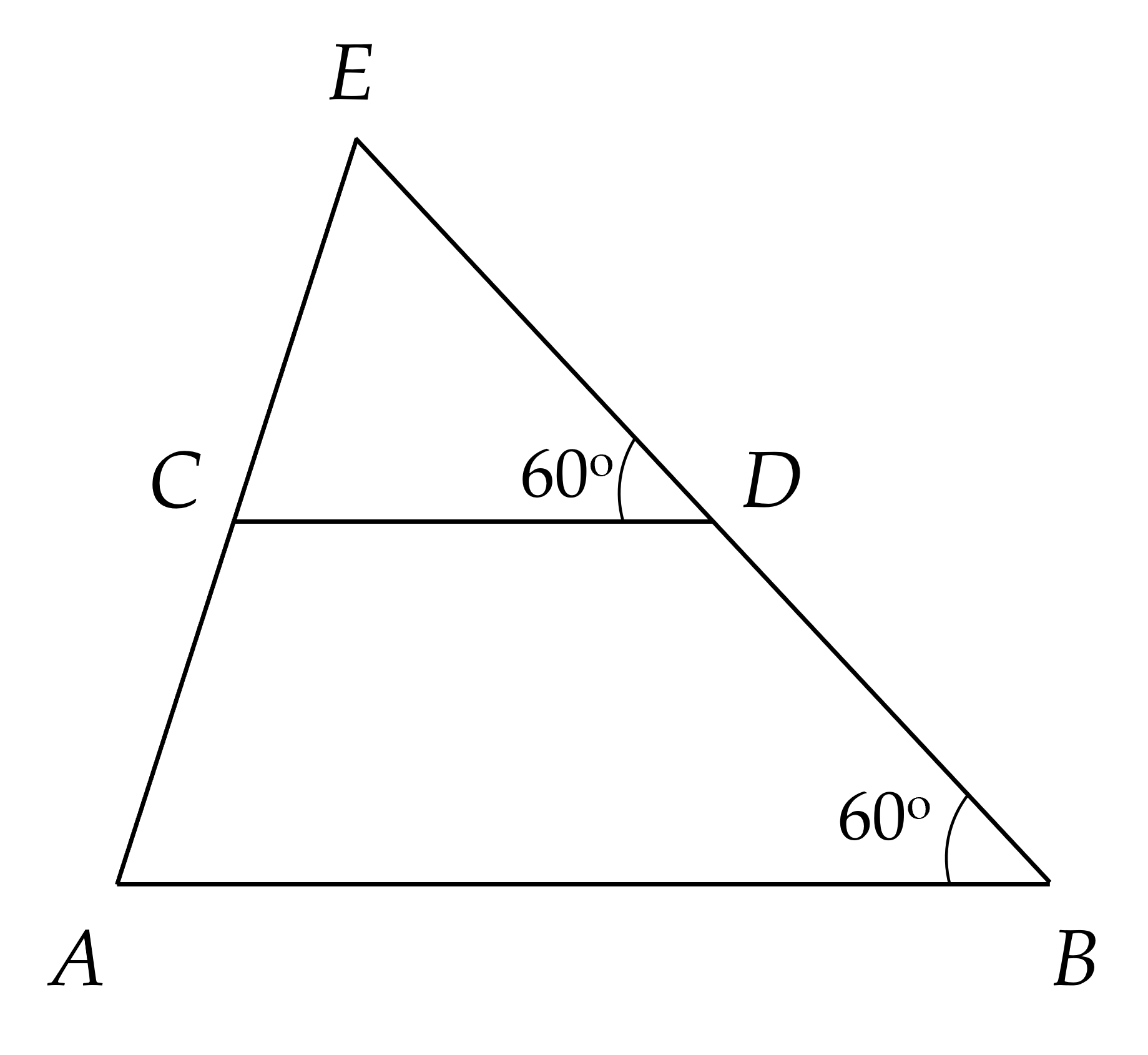
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

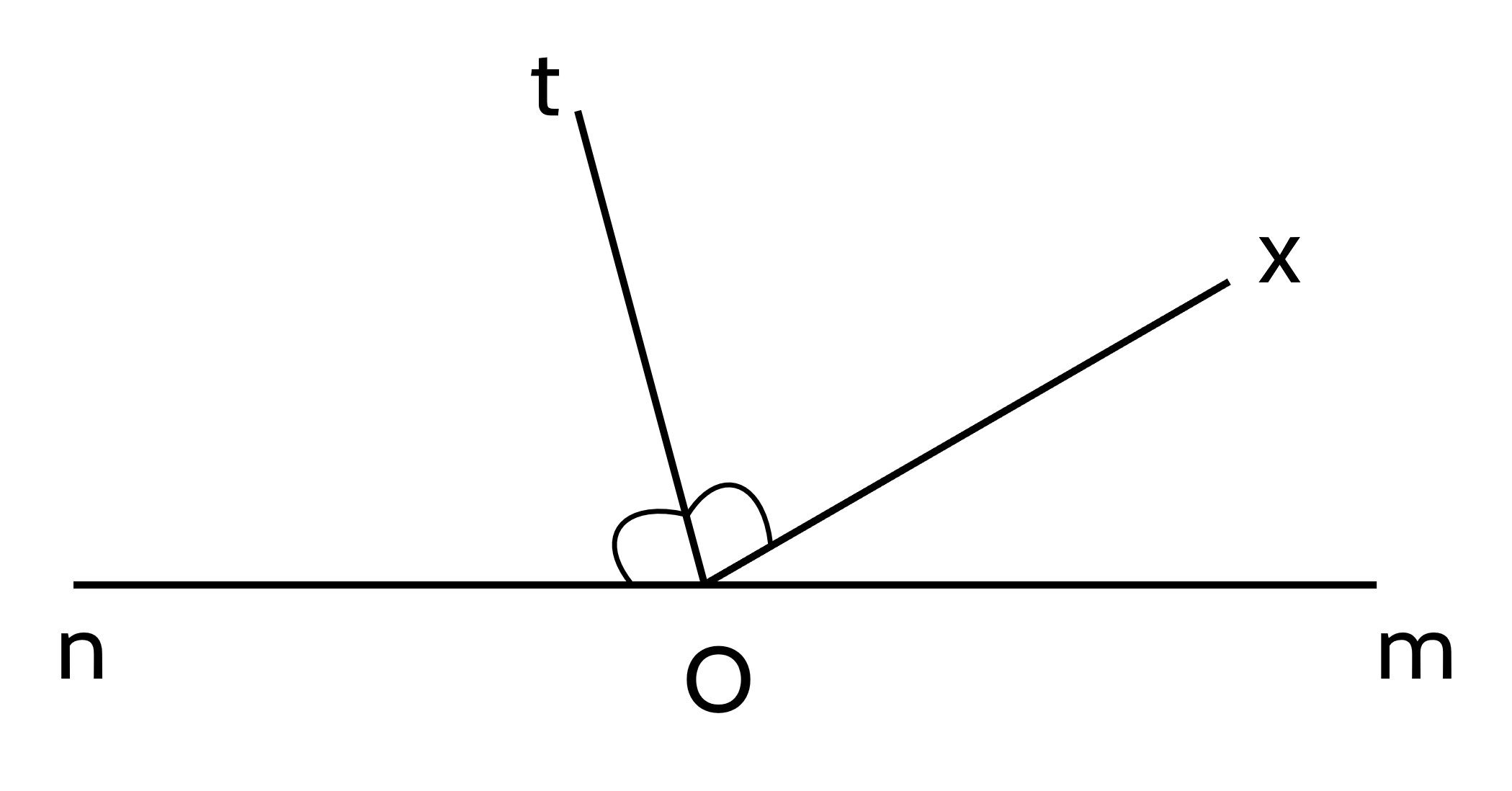
a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
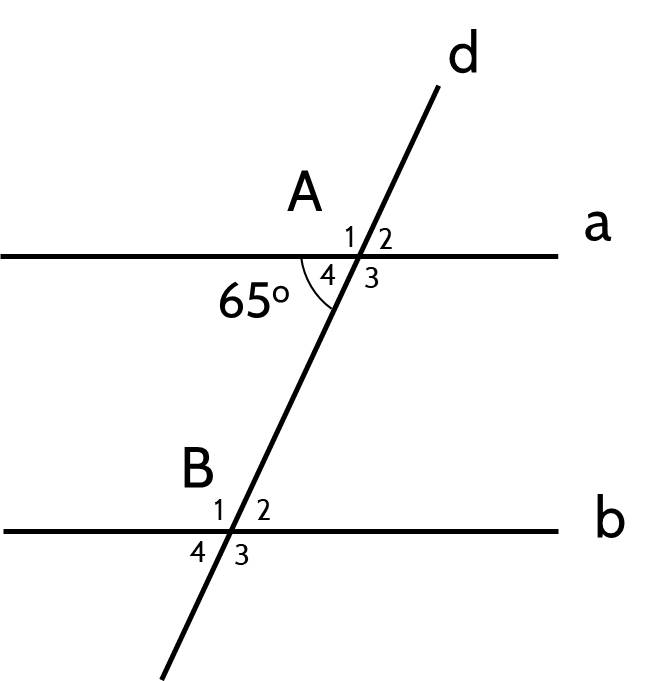
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65∘ (hai góc so le trong).
Mặt khác, ta có �2^+�3^=180∘B2+B3=180∘
Suy ra �3^=180∘−�2^=115∘B3=180∘−B2=115∘.

- Kẻ AH⊥aAH⊥a kéo dài, HA cắt b tại B.
- Kẻ AK⊥bAK⊥b kéo dài KA cắt a tại C.
- Kẻ AI⊥BCAI⊥BC, đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên OA⊥BCOA⊥BC
AI⊥BCAI⊥BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.

Nếp gấp zt vuông góc với đường thẳng xy tại O. Có bốn góc vuông là xOz,yOz,yOt,tOx.

Vì AD=AE
nên A nằm trên đường phân giác của góc xOy
Vì BM=BN
nên B nằm trên đường phân giác của góc xOy
=>AB là phân giác của góc xOy

a)
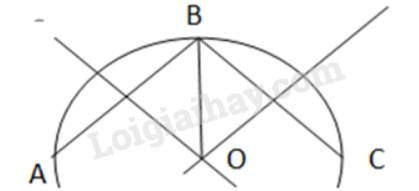
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.
- Bán kính đường tròn cần tìm là độ dài đoạn OB (hoặc OA hoặc OC).
b)
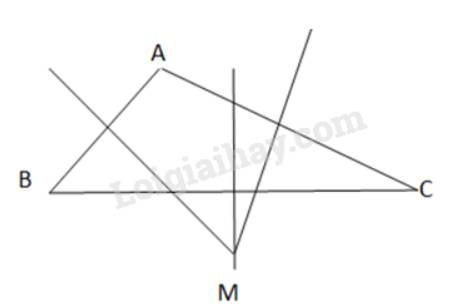
- Bước 1: Vẽ đường trung trực của các đoạn AB, AC, BC
- Bước 2: 3 đường trung trực này cắt nhau tại M. Khi đó MA= MB=MC.
- Bước 3: M là điểm cần xác định.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)







Gọi giao điểm của AB và xy là O
\( \Rightarrow \) O là trung điểm AB (Do xy là đường trung trực của AB)
\( \Rightarrow \) Đo khoảng cách AO và từ điểm O kẻ OB sao cho OA = OB và nằm khác phía với điểm A so với đường thẳng xy (A, B, O thẳng hàng)