QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Cặp tam giác bằng nhau là:
\(\Delta ABC = \Delta MNP\) vì
\(\begin{array}{l}\widehat B = \widehat N( = 50^\circ )\\BC = NP\\\widehat C = \widehat P( = 70^\circ )\end{array}\)
Vậy \(\Delta ABC = \Delta MNP\) (g-c-g)
TT
1
28 tháng 1 2022
phải có hình hoặc số đo cạnh hoặc góc thì mới so sánh đc chứ
3 tháng 11 2016
tam giác ABC và tam giác HIK . vì AB = KI , góc B = góc K .
suy ra : AC=IH ; BC = KH
CM
26 tháng 11 2019
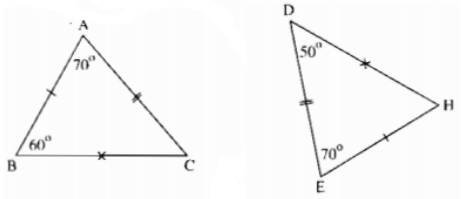
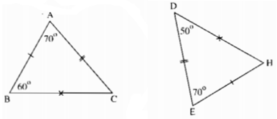
ΔABC có: ∠C = 180o - ∠A - ∠B = 50o
ΔEDH có: ∠H = 180o - ∠D - ∠E = 60o
Có: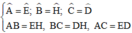 
Vậy ΔABC = ΔEHD
14 tháng 3 2022
1.Khẳng định nào sau đây không đúng:
A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó
B. Trong tam giác cân hai góc ở đáy bằng nhau
C. Tam giác có hai góc bằng nhau là tam giác đều
2.Tam giác nào là tam giác vuông với số đo 3 cạnh như sau:
A. 13m; 14m; 15m B. 11m; 12m; 10m
C. 12m; 9m; 15m D. 8m; 8m; 10m
D. Trong tam giác đều mỗi góc bằng 60 độ
CM
26 tháng 6 2019
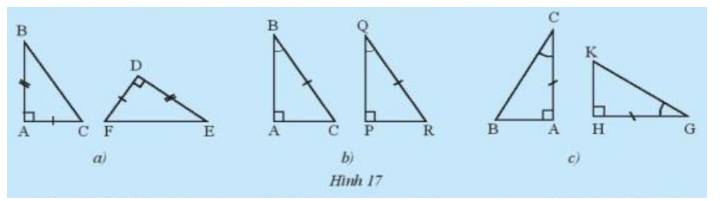
a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
TT
2
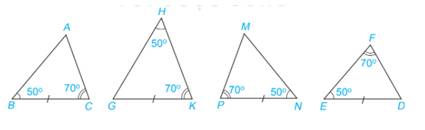
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)