TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
2
H
1
PT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
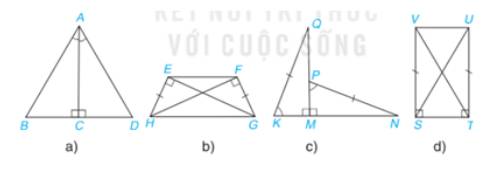
a) Xét 2 tam giác vuông ABC và ADC có:
\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)
AC chung
\(\widehat {BAC} = \widehat {DAC}\)(gt)
=>\(\Delta ABC = \Delta ADC\)(g.c.g)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
=>\(\Delta HEG = \Delta GFH\)(cạnh huyền - cạnh góc vuông)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP(gt)
\(\widehat K = \widehat P\)(gt)
=>\(\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT(gt)
ST chung
=>\(\Delta VST = \Delta UTS\)(2 cạnh góc vuông)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
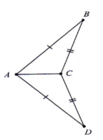
a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:
AC = CE
\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )
CB = CD
\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)
b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì
\(AC \ne BE;BC \ne BD;DE \ne AC\)
GL
21 tháng 9 2023
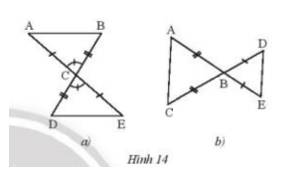
* Hình 14a:
Xét ∆ABC và ∆EDC có:
BC = DC (giả thiết);
^ACB = ^ECD (hai góc đối đỉnh);
AC = EC (giả thiết).
Do đó ∆ABC = ∆EDC (c.g.c).
* Hình 14b:
Không có cạnh nào của tam giác ABC bằng với cạnh của tam giác EBD nên hai tam giác này không bằng nhau.
Vậy Hình 14a có ∆ABC = ∆EDC (c.g.c); Hình 14b hai tam giác ABC và EBC không bằng nhau.
PT
1
CM
26 tháng 6 2019
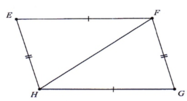
a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)
PT
1
CM
4 tháng 3 2019
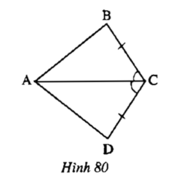
ΔABC và ΔADC có
AC chung
Góc ACB = góc DCB
BC = DC
⇒ ΔABC = ΔADC ( cạnh – góc – cạnh)
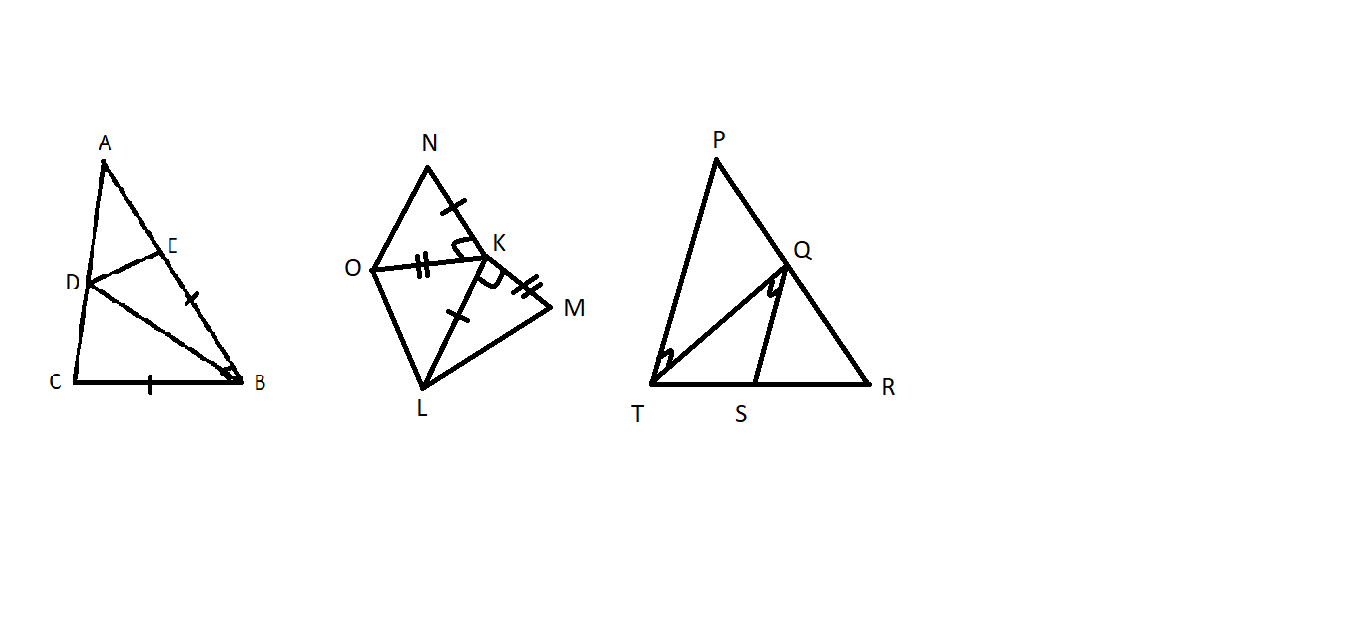
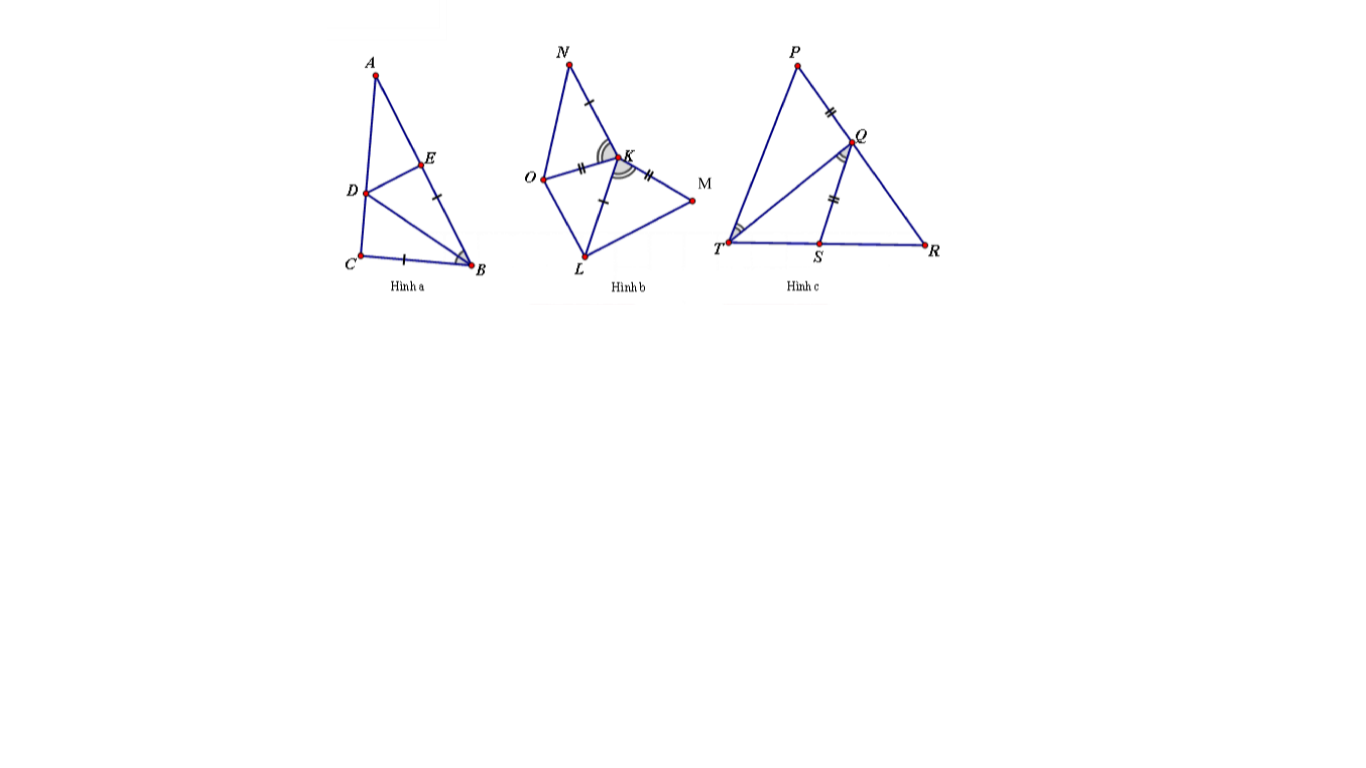
phải có hình hoặc số đo cạnh hoặc góc thì mới so sánh đc chứ