Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Rightarrow1-\dfrac{b}{a}=1-\dfrac{d}{c}\Rightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\) (đpcm)

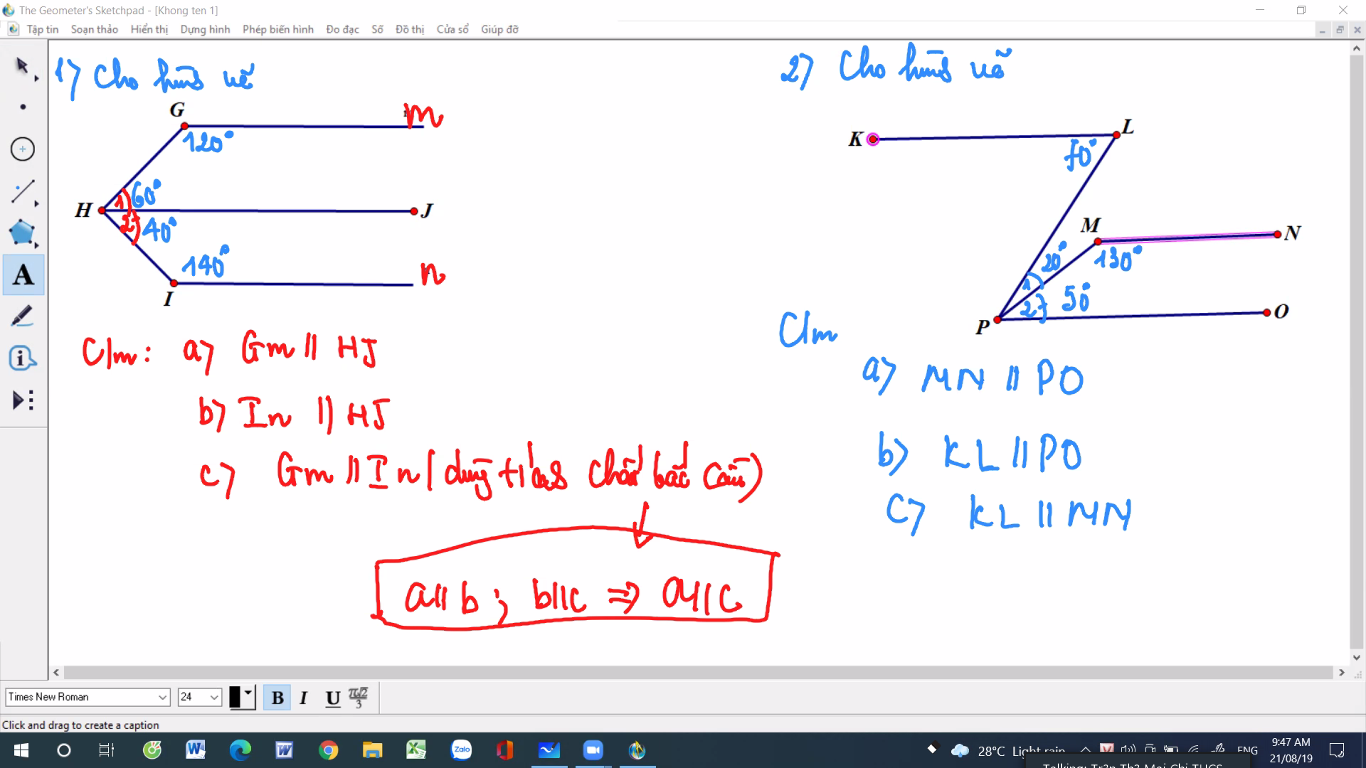
cặp : Ea// Fb (vì góc e +góc f =180 mà 2 góc này ở vị trí trong cùng phía)
cặp Fb // DC (vì có góc F = góc D (=110) mà 2 góc này ở vị trí đồng vị)
cặp : Ea //DC vì Ea // Fb, Fb //DC (tính chất bắc cầu)
\(\\ \)

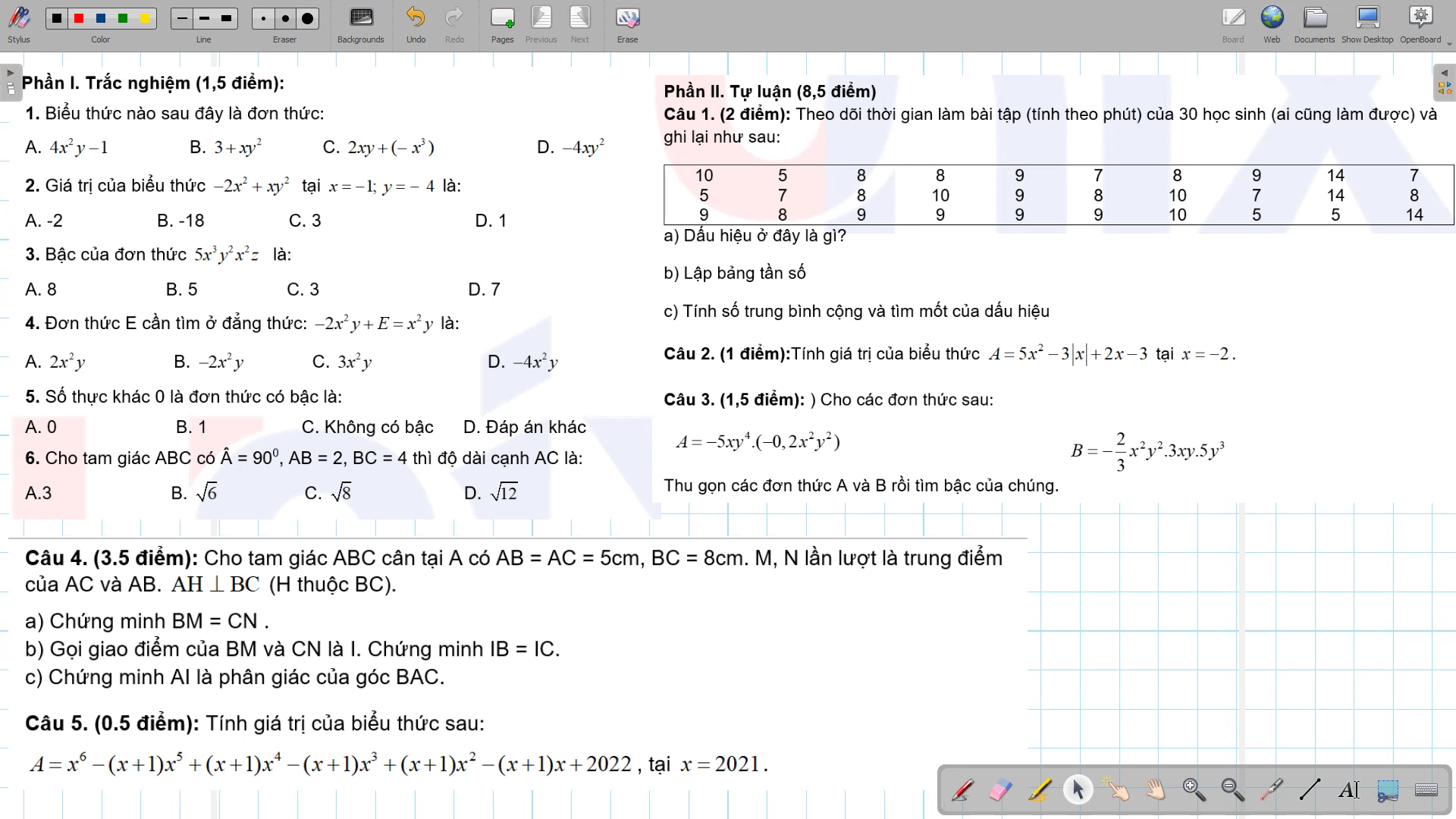
4:
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc IBC=góc ICB
=>IB=IC
c: Xét ΔABI và ΔACI có
AB=AC
IB=IC
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC

Ta đánh số điểm từ 1 đến 10
Điểm 1 tạo với 9 điểm còn lại được 8 tam giác
Điểm 2 tạo với 8 điểm còn lại (trừ điểm 1) được 7 tam giác
Điểm 3 tạo với 7 điểm còn lại (trừ điểm 1 và điểm 2) được 7 tam giác
...................................
Vậy số tam giác được tạo ra từ 10 điểm trên là:
8+7+6+..+1+0=36 (tam giác)


a: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
b: Ta có: ΔBAK=ΔBDK
nên KA=KD
mà BA=BD
nên BK là đường trung trực của AD
a)Xét \(\Delta BAK\) và \(\Delta BDK\) có:
AB=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
=> \(\Delta BAK\) = \(\Delta BDK\) (c-g-c)
b)Gọi O là giao điểm của AD và BK
Xét \(\Delta ABO\) và \(\Delta DBO\) có :
BO chung
\(\widehat{ABO}=\widehat{DBO}\)
AB=DB
=> \(\Delta ABO\) và \(\Delta DBO\) (c-g-c)
=> AO=BO (1) ; \(\widehat{AOB}=\widehat{DOB}\)
Có : \(\widehat{AOB}+\widehat{DOB}=180^o\) mà \(\widehat{AOB}=\widehat{DOB}\)
=> \(\widehat{AOB}=\widehat{DOB}=\dfrac{180^o}{2}=90^o\) (2)
Từ (1)(2) => BK là đường trung trực cùa AD

\(\dfrac{1}{3\times5}=\dfrac{2}{3}-\dfrac{3}{5}\)
\(\dfrac{1}{5\times7}=\dfrac{3}{5}-\dfrac{4}{7}\)

x+1/3+x+14/43+x+1/19+x+26=0
4x+65470/2451=0
4x=-65470/2451
x=-32735/4902