K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 10 2023
a: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔDSB có
M,O lần lượt là trung điểm của DS,DB
Do đó: MO là đường trung bình
=>MO//SB và MO=SB/2
SB//MO
\(MO\subset\left(MAC\right)\)
SB không nằm trong mp(MAC)
Do đó: SB//(MAC)
b: Xét ΔABC có
N,O lần lượt là trung điểm của AB,AC
=>NO là đường trung bình
=>NO//BC
mà BC\(\subset\left(SBC\right)\)
và NO không nằm trong mp(SBC)
nên NO//(SBC)
MO//SB
\(SB\subset\left(SBC\right)\)
MO không nằm trong (SBC)
Do đó: MO//(SBC)
mà NO//(SBC)
và \(MO,NO\subset\left(MON\right)\)
nên \(\left(MON\right)\)//(SBC)
=>MN//(SBC)
22 tháng 11 2023
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{x+6}-\sqrt{x+2}}{x^2-4}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{x+6}-2+2-\sqrt{x+2}}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{x+6-8}{\sqrt[3]{\left(x+6\right)^2}+2\cdot\sqrt[3]{x+6}+4}+\dfrac{4-x-2}{2+\sqrt{x+2}}}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(\dfrac{1}{\sqrt[3]{\left(x+6\right)^2}+2\sqrt[3]{x+6}+4}-\dfrac{1}{2+\sqrt{x+2}}\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{1}{\sqrt[3]{\left(x+6\right)^2}+2\cdot\sqrt[3]{x+6}+4}-\dfrac{1}{2+\sqrt{x+2}}}{x+2}\)
\(=\dfrac{\dfrac{1}{\sqrt[3]{\left(2+6\right)^2}+2\cdot\sqrt[3]{2+6}+4}-\dfrac{1}{2+\sqrt{2+2}}}{2+2}\)
\(=\dfrac{\dfrac{1}{\sqrt[3]{64}+2\cdot\sqrt[3]{8}+4}-\dfrac{1}{2+2}}{4}\)
\(=\dfrac{\dfrac{1}{4+2\cdot2+4}-\dfrac{1}{4}}{4}=\left(\dfrac{1}{16}-\dfrac{1}{4}\right):4=\left(\dfrac{1}{16}-\dfrac{4}{16}\right)\cdot\dfrac{1}{4}=\dfrac{-3}{64}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
c.
ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)
\(1-\dfrac{\sqrt{3}cosx}{sinx}-4cosx=0\)
\(\Rightarrow sinx-\sqrt{3}cosx-4sinx.cosx=0\)
\(\Leftrightarrow sinx-\sqrt{3}cosx=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=sin2x\)
\(\Leftrightarrow sin2x=sin\left(x-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x-\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{4\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{4\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
a.
\(\Leftrightarrow3sin3x-4sin^34x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow sin9x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sin9x-\dfrac{\sqrt{3}}{2}cos9x=sin2x\)
\(\Leftrightarrow sin\left(9x-\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}9x-\dfrac{\pi}{3}=2x+k2\pi\\9x-\dfrac{\pi}{3}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{21}+\dfrac{k2\pi}{7}\\x=\dfrac{4\pi}{33}+\dfrac{k2\pi}{11}\end{matrix}\right.\)
TV
help me giúp giúp mình với ạ
0
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
1.
\(-1\le sin\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=-1\)
\(y_{max}=5\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=1\)
2.
\(-1\le cos2x\le1\Rightarrow\dfrac{5}{2}\le y\le\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi \(cos2x=1\)
\(y_{max}=\dfrac{7}{2}\) khi \(cos2x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
3.
\(0\le cos^2\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le-1\)
\(y_{min}=-2\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=\pm1\)
\(y_{max}=-1\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=0\)
4.
\(-1\le cos\left(4x^2\right)\le1\Rightarrow-2\le y\le\sqrt{2}-2\)
\(y_{min}=-1\) khi \(cos\left(4x^2\right)=-1\)
\(y_{max}=\sqrt{2}-2\) khi \(cos\left(4x^2\right)=1\)
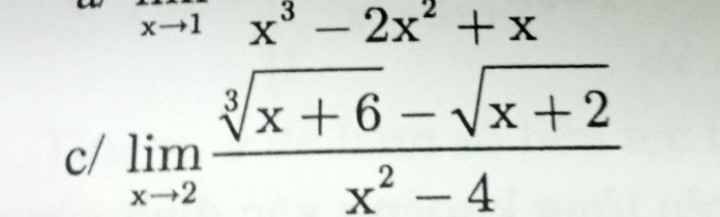
D