
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c.
ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)
\(1-\dfrac{\sqrt{3}cosx}{sinx}-4cosx=0\)
\(\Rightarrow sinx-\sqrt{3}cosx-4sinx.cosx=0\)
\(\Leftrightarrow sinx-\sqrt{3}cosx=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=sin2x\)
\(\Leftrightarrow sin2x=sin\left(x-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x-\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{4\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{4\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
a.
\(\Leftrightarrow3sin3x-4sin^34x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow sin9x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sin9x-\dfrac{\sqrt{3}}{2}cos9x=sin2x\)
\(\Leftrightarrow sin\left(9x-\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}9x-\dfrac{\pi}{3}=2x+k2\pi\\9x-\dfrac{\pi}{3}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{21}+\dfrac{k2\pi}{7}\\x=\dfrac{4\pi}{33}+\dfrac{k2\pi}{11}\end{matrix}\right.\)



1.
\(-1\le sin\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=-1\)
\(y_{max}=5\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=1\)
2.
\(-1\le cos2x\le1\Rightarrow\dfrac{5}{2}\le y\le\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi \(cos2x=1\)
\(y_{max}=\dfrac{7}{2}\) khi \(cos2x=-1\)
3.
\(0\le cos^2\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le-1\)
\(y_{min}=-2\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=\pm1\)
\(y_{max}=-1\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=0\)
4.
\(-1\le cos\left(4x^2\right)\le1\Rightarrow-2\le y\le\sqrt{2}-2\)
\(y_{min}=-1\) khi \(cos\left(4x^2\right)=-1\)
\(y_{max}=\sqrt{2}-2\) khi \(cos\left(4x^2\right)=1\)

\(\lim\limits\left(2-3n\right)^4\left(n+1\right)^3=\lim n^7\left(3-\dfrac{2}{n}\right)^4\left(1+\dfrac{1}{n}\right)^3=+\infty\)
\(\lim\left(\sqrt[3]{n+4}-\sqrt[3]{n+1}\right)=\lim\dfrac{3}{\sqrt[3]{\left(n+4\right)^2}+\sqrt[3]{\left(n+4\right)\left(n+1\right)}+\sqrt[3]{\left(n+1\right)^2}}=0\)
\(\lim\left(\sqrt[3]{8n^3+3n^2+4}-2n+6\right)=\lim\dfrac{8n^3+3n^2+4-\left(2n-6\right)^3}{\sqrt[3]{\left(8n^3+3n^2+4\right)^2}+\left(2n-6\right)\sqrt[3]{8n^3+3n^2+4}+\left(2n-6\right)^2}\)
\(=\lim\dfrac{75n^2-216n+220}{\sqrt[3]{\left(8n^3+3n^2+4\right)^2}+\left(2n-6\right)\sqrt[3]{8n^3+3n^2+4}+\left(2n-6\right)^2}\)
\(=\lim\dfrac{75-\dfrac{216}{n}+\dfrac{220}{n^2}}{\sqrt[3]{\left(8+\dfrac{3}{n}+\dfrac{4}{n^3}\right)^2}+\left(2-\dfrac{6}{n}\right)\sqrt[3]{8+\dfrac{3}{n}+\dfrac{4}{n^3}}+\left(2-\dfrac{6}{n}\right)^2}\)
\(=\dfrac{75}{\sqrt[3]{8^2}+2.\sqrt[3]{8}+2^2}=...\)
d.
\(\lim\left(\sqrt[3]{8n^3+3n^2-2}+\sqrt[3]{5n^2-8n^3}\right)\)
\(=\lim\left(\sqrt[3]{8n^3+3n^2-2}-\sqrt[3]{8n^3-5n^2}\right)\)
\(=\lim\dfrac{8n^3+3n^2-2-\left(8n^3-5n^2\right)}{\sqrt[3]{\left(8n^3+3n^2-2\right)^2}+\sqrt[3]{\left(8n^3+3n^2-2\right)\left(8n^3-5n^2\right)}+\sqrt[3]{8n^3-5n^2}}\)
\(=\lim\dfrac{8n^2-2}{\sqrt[3]{\left(8n^3+3n^2-2\right)^2}+\sqrt[3]{\left(8n^3+3n^2-2\right)\left(8n^3-5n^2\right)}+\sqrt[3]{8n^3-5n^2}}\)
\(=lim\dfrac{8-\dfrac{2}{n^2}}{\sqrt[3]{\left(8+\dfrac{3}{n}-\dfrac{2}{n^3}\right)^2}+\sqrt[3]{\left(8+\dfrac{3}{n}-\dfrac{2}{n^3}\right)\left(8-\dfrac{5}{n}\right)}+\sqrt[3]{\left(8-\dfrac{5}{n}\right)^2}}\)
\(=\dfrac{8}{\sqrt[3]{8^2}+\sqrt[3]{8.8}+\sqrt[3]{8^2}}=...\)

Lời giải:
Ta có:
\(f'(x)=3x^2+2(a-1)x+2\)
Theo định lý về dấu của tam thức bậc 2, để \(f'(x)>0\) với mọi \(x\in\mathbb{R}\) thì \(\Delta'=(a-1)^2-6<0\)
\(\Leftrightarrow -\sqrt{6}< a-1< \sqrt{6}\)
\(\Leftrightarrow 1-\sqrt{6}< a< 1+\sqrt{6}\)
Đáp án B

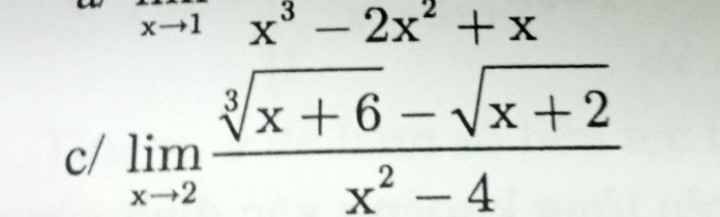


\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{x+6}-\sqrt{x+2}}{x^2-4}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{x+6}-2+2-\sqrt{x+2}}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{x+6-8}{\sqrt[3]{\left(x+6\right)^2}+2\cdot\sqrt[3]{x+6}+4}+\dfrac{4-x-2}{2+\sqrt{x+2}}}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(\dfrac{1}{\sqrt[3]{\left(x+6\right)^2}+2\sqrt[3]{x+6}+4}-\dfrac{1}{2+\sqrt{x+2}}\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{1}{\sqrt[3]{\left(x+6\right)^2}+2\cdot\sqrt[3]{x+6}+4}-\dfrac{1}{2+\sqrt{x+2}}}{x+2}\)
\(=\dfrac{\dfrac{1}{\sqrt[3]{\left(2+6\right)^2}+2\cdot\sqrt[3]{2+6}+4}-\dfrac{1}{2+\sqrt{2+2}}}{2+2}\)
\(=\dfrac{\dfrac{1}{\sqrt[3]{64}+2\cdot\sqrt[3]{8}+4}-\dfrac{1}{2+2}}{4}\)
\(=\dfrac{\dfrac{1}{4+2\cdot2+4}-\dfrac{1}{4}}{4}=\left(\dfrac{1}{16}-\dfrac{1}{4}\right):4=\left(\dfrac{1}{16}-\dfrac{4}{16}\right)\cdot\dfrac{1}{4}=\dfrac{-3}{64}\)