
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1100}{x}-\dfrac{1100}{x+5}=2\)
\(\Leftrightarrow\dfrac{1105-1100}{x+5}=2\)
\(\Leftrightarrow\dfrac{5}{x-5}=2\)
\(\Leftrightarrow5=2\left(x-5\right)\)
\(\Leftrightarrow5=2x-10\)
\(\Leftrightarrow2x=15\)
\(\Leftrightarrow x=\dfrac{15}{2}=7,5\)
\(\dfrac{1100}{x}-\dfrac{1100}{x+5}=2\left(ĐK:x\ne0;x\ne-5\right)\\ \Leftrightarrow\dfrac{1100\left(x+5\right)-1100x}{x\left(x+5\right)}=\dfrac{2x\left(x+5\right)}{x\left(x+5\right)}\\ \Leftrightarrow2x^2+10x-5500=0\\ \Leftrightarrow2x^2-100x+110x-5500=0\\ \Leftrightarrow2x.\left(x-50\right)+110.\left(x-50\right)=0\\ \Leftrightarrow\left(2x+110\right).\left(x-50\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+110=0\\x-50=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-55\left(TM\right)\\x=50\left(TM\right)\end{matrix}\right.\)
Vậy: S={-55;50}

\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\\left(x+y\right)-3\sqrt{x+1}=-5\end{matrix}\right.\left(x\ge-1\right)\)
Đặt \(\left\{{}\begin{matrix}a=x+y\\b=\sqrt{x+1}\end{matrix}\right.\left(b\ge0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}2a+b=4\\a-3b=-5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2a+b=4\left(1\right)\\2a-6b=-10\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow7b=14\Rightarrow b=2\Rightarrow2a=4-2=2\Rightarrow a=1\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=1\\\sqrt{x+1}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-2\\x=3\end{matrix}\right.\)

Bạn cần giúp bài nào ạ? Nếu bạn cần giúp hết, bạn tách các câu ra từng CH riêng nhé, không ai làm hết được tất cả trong 1 CH đâu bạn, mà có làm thì chất lượng cũng chưa được cao.

Lời giải:
\(C=\frac{x+\sqrt{x}+17}{x+\sqrt{x}}=1+\frac{17}{x+\sqrt{x}}\)
Để $C$ nhỏ nhất thì $\frac{17}{x+\sqrt{x}$ nhỏ nhất
Tức là $x+\sqrt{x}$ lớn nhất với mọi $x\geq 0$
Khi $x\geq 0$ thì ta không thể tìm GTLN của $x+\sqrt{x}$ vì cứ cho $x$ tăng vô hạn thì $x+\sqrt{x}$ cũng tăng vô hạn.
Vì vậy biểu thức C không có min bạn nhé. Bạn cần bổ sung thêm điều kiện khác về $x$ để tìm.

ĐK: \(x\ge0\)
Lấy P - 1
\(\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}-1\)
\(=\dfrac{\sqrt{x}-2-2\sqrt{x}-1}{2\sqrt{x}+1}\)
\(=\dfrac{-\sqrt{x}-3}{2\sqrt{x}+1}\)
\(=\dfrac{-\left(\sqrt{x}+3\right)}{2\sqrt{x}+1}\)
Ta thấy \(\left\{{}\begin{matrix}\sqrt{x}+3>0\\2\sqrt{x}+1>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-\left(\sqrt{x}+3\right)< 0\\2\sqrt{x}+1>0\end{matrix}\right.\Rightarrow P-1< 0\)
Vậy \(P< 1\).


Ta có:
n3 + 11n
= n3 - n + 12n
= n.(n2 - 1) + 12n
= n.(n - 1).(n + 1) + 12n
= (n - 1).n.(n + 1) + 12n
Vì (n - 1).n.(n + 1) là tích 3 số tự nhiên liên tiếp => tích này chia hết cho 2 và 3
Mà (2;3)=1 => (n - 1).n.(n + 1) chia hết cho 6; 12n chia hết cho 6
=> n3 + 11n chia hết cho 6 ( đpcm)

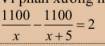

 Làm hộ mk bài 1 nhé! Thank các bạn nhiều!!!!
Làm hộ mk bài 1 nhé! Thank các bạn nhiều!!!!


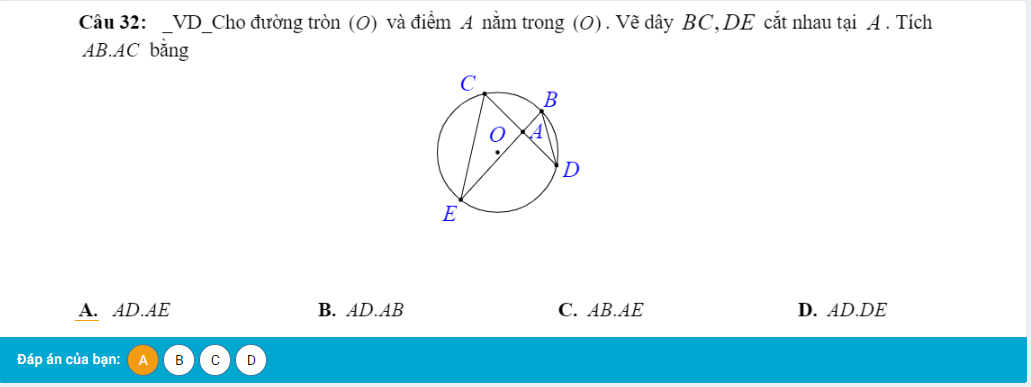
a: góc HIB+góc HKB=180 độ
=>HIBK nội tiếp
b: Xét ΔAHM và ΔAMK có
góc AMH=góc AKM
góc HAM chung
=>ΔAHM đồng dạng với ΔAMK
c: AH*AK+BI*BA
=AI*AB+BI*BA
=AB^2
=4R^2