Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\hept{\begin{cases}mx+4y=10-m\left(1\right)\\x+my=4\left(2\right)\end{cases}}\)
từ (2) ta có \(x=4-my\) (3)
thay (3) vào (1) ta có \(m\left(4-my\right)+4y=10-m\)
\(\Leftrightarrow4m-m^2y+4y=10-m\)
\(\Leftrightarrow y\left(4-m^2\right)=10-m-4m\)
\(\Leftrightarrow y\left(4-m^2\right)=10-5m\) \(\left(4\right)\)
để hpt có nghiệm duy nhất thì pt (4) pải có nghiệm duy nhất
\(\Leftrightarrow4-m^2\ne0\Leftrightarrow m^2\ne4\Leftrightarrow m\ne\pm2\)
từ (4) ta có \(y=\frac{10-5m}{4-m^2}\)
\(y=\frac{5m-10}{m^2-4}\)
\(y=\frac{5\left(m-2\right)}{\left(m+2\right)\left(m-2\right)}\)
\(y=\frac{5}{m+2}\)
từ (3) ta có \(x=4-\frac{5m}{m+2}\)
\(x=\frac{4m+8-5m}{m+2}\)
\(x=\frac{8-m}{m+2}\)
theo bài ra \(S=x^2-y^2\)
\(S=\left(\frac{8-m}{m+2}\right)^2-\left(\frac{5}{m+2}\right)^2\)
\(S=\left(\frac{8-m-5}{m+2-m-2}\right)\left(\frac{8-m+5}{m+2+m+2}\right)\)
\(S=\left(3-m\right)\left(\frac{13-m}{2m+4}\right)\)
\(S=\frac{\left(3-m\right)\left(13-m\right)}{2m+4}\)
\(S=\frac{39-3m-13m+m^2}{2m+4}\)
\(S=\frac{m^2-16m+39}{2m+4}\)
Bài 2:
Ta có: \(A=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)
\(=\dfrac{\sqrt{6+2\sqrt{5}}+\sqrt{14-6\sqrt{5}}-2}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}+1+3-\sqrt{5}-2}{\sqrt{2}}=\sqrt{2}\)
Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\m\left(2-my\right)-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\2m-m^2y-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\2m-\left(m^2y+2y\right)=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\m^2y+2y=2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\y\left(m^2+2\right)=2m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-\dfrac{m\cdot\left(2m-1\right)}{m^2+2}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m^2+4-2m^2+m}{m^2+2}=\dfrac{m+4}{m^2+2}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Tới đây bạn tự làm tiếp nhé
Lời giải:
a.
Từ $x+y=2\Rightarrow y=2-x$. Thay vào PT(2):
$(m+1)x+m(2-x)=7$
$\Leftrightarrow x+2m=7$
$\Leftrightarrow x=7-2m$
$y=2-x=2-(7-2m)=2m-5$
Vậy hpt có nghiệm $(x,y)=(7-2m, 2m-5)(*)$
Nếu $x,y$ có 1 số $\geq 0$, một số $\leq 0$ thì $xy\leq 0< 1$
Nếu $x,y$ cùng $\geq 0$ thì áp dụng BĐT Cô-si:
$2=x+y\geq 2\sqrt{xy}\Rightarrow xy\leq 1$
Vậy tóm lại $xy\leq 1(**)$
Từ $(*); (**)$ suy ra với mọi $m$ thì hpt luôn có nghiệm $x,y$ thỏa mãn $xy\leq 1$
b.
$xy>0$
$\Leftrightarrow (7-2m)(2m-5)>0$
$\Leftrightarrow 7> 2m> 5$
$\Leftrightarrow \frac{7}{2}> m> \frac{5}{2}$
Do $m$ nguyên nên $m=3$
Thử lại thấy đúng.
Chọn đáp án B
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: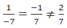
⇒ Hệ pt vô nghiệm