
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3}y-\dfrac{5}{3}x+5-\dfrac{1}{4}y-\dfrac{27}{4}+2x=0\\\dfrac{1}{3}x+\dfrac{1}{3}+y-\dfrac{6}{7}y+\dfrac{5}{7}x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}x+\dfrac{1}{28}y=-5\\\dfrac{22}{21}x+\dfrac{1}{7}y=-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}28x+3y=-420\\88x+12y=-28\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}112x+12y=-420\\88x+12y=-28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x=-392\\28x+3y=-420\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{49}{3}\\y=\dfrac{112}{9}\end{matrix}\right.\)

\(\hept{\begin{cases}\frac{7}{x-y+2}-\frac{5}{x+y-1}=\frac{9}{2}\\\frac{3}{x-y+2}+\frac{2}{x+y-1}=4\end{cases}}\)
Đặt \(a=\frac{1}{x-y+2};b=\frac{1}{x+y-1}\)ta được hệ phương trình:
\(\hept{\begin{cases}7a-5b=\frac{9}{2}\\3a+2b=4\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=\frac{1}{2}\end{cases}}}\)
Với \(\hept{\begin{cases}a=1\\b=\frac{1}{2}\end{cases}}\), ta được:
\(\hept{\begin{cases}\frac{1}{x-y+2}=1\\\frac{1}{x+y-1}=\frac{1}{2}\end{cases}\Leftrightarrow}\hept{\begin{cases}x-y+2=1\\x+y-1=2\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}}\)
Vậy hệ phương trình có 1 nghiệm là x = 1 và y = 2

Ta có: x -3y =2
<=> 2x-6y =4 (1)
* 2x-5y= -1 (2)
Phương trình (1) -pt (2) ta có:
2x -6y -(2x-5y) =4-(-1)
<=> 2x- 6y -2x+5y =5
<=>y= -5
Thay y= -5 vào pt (2) ta có:
2.x -5.(-5) =-1
<=>2x +25 =-1
<=> 2x=-26
<=> x=-13
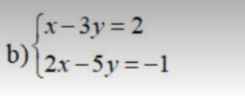 giải hệ phương trình
giải hệ phương trình
Ta có: \(\hept{\begin{cases}4+b=1\\-2a+b=7\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}b=3\\-2a+3=7\end{cases}\Rightarrow\hept{\begin{cases}b=3\\a=-2\end{cases}}}\)
Vậy \(\hept{\begin{cases}b=3\\a=-2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}4+b=1\\-2a+b=7\end{cases}\Rightarrow\hept{\begin{cases}b=-3\\-2a-3=7\end{cases}\Rightarrow}\hept{\begin{cases}b=-3\\a=-5\end{cases}}}\)
Vậy \(\hept{\begin{cases}a=-3\\b=-5\end{cases}}\)
Hok tốt