Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{a}{b}=\frac{a.\left(-1\right)}{b.\left(-1\right)}=\frac{-a}{-b}\)
\(\frac{-a}{-\left(-b\right)}=\frac{-a}{b}\)
2 kết quả này ko giống nhau
Vậy bạn đó giải sai
Vì b < 0 nên ta có phân số \(\frac{a}{b}=\frac{-a}{-b}\)
Khi đó a < 0 và b > 0
Do đó \(\frac{a}{b}=\frac{a.\left(-1\right)}{b.\left(-1\right)}=\frac{-a}{-b}\)
Vì \(\frac{-a}{-b}\ne\frac{-a}{-\left(-b\right)}\)
Do vậy bạn đó tính sai

\(\frac{20}{-35}=\frac{20.\left(-1\right)}{-35.\left(-1\right)}=\frac{-20}{35}\)
\(\frac{2}{-3}=\frac{2.\left(-1\right)}{-3.\left(-1\right)}=\frac{-2}{3}\)
\(\frac{ab}{-cd}=\frac{ab.\left(-1\right)}{-cd.\left(-1\right)}=\frac{-ab}{cd}\)
ta chỉ cần nhân cả tử & mẫu với -1
hay nói cách khác là đổi dấu của cả tử & mẫu

a) 3 − 4 = − 3 4
b) − 5 − 17 = 5 17
c) m n = − m − n ( m , n ∈ Z , m < 0 )

Bài 1:
a: 3/-5=-3/5=-6/10
b: 5/-10=-1/2=-5/10
c: -4/-9=4/9=8/18
d: -6/8=-3/4=-9/12
e: 0/-10=0
f: 0/-6=0

a ) 3 − 5 = 6 10 = − 9 15 b ) 5 10 = − 1 2 = − 2 4
c ) − 4 − 9 = 8 18 = 12 27 d ) − 6 − 8 = 3 4 = 9 12
e ) 0 − 10 = 0 2 = 0 3 f ) 0 − 6 = 0 2 = 0 3

a ) 1 − 8 = − 2 16 = − 3 24 b ) 3 − 6 = − 1 2 = − 2 4
c ) − 7 − 8 = 14 16 = 21 24 d ) − 12 − 15 = 4 5 = 8 10
e ) 0 − 11 = 0 2 = 0 3 f ) 0 − 103 = 0 2 = 0 3

a)\(\frac{2}{-7}=\frac{-2}{7}\)
b) \(\frac{-3}{-11}=\frac{3}{11}\)
c) \(\frac{6}{-29}=\frac{-6}{29}\)
d) \(\frac{0}{-14}=\frac{0}{14}\)

a) 2 − 5 = − 3 5 = − 6 10 ;
b) 5 − 10 = − 5 10 = − 10 20 ;
c) − 6 − 8 = 6 8 = 12 16 ;
d) 0 − 10 = 0 10 = 0 20
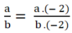
ta nhân cả từ và mẫu của phân số \(\frac{a}{b}\) với -1
\(\frac{a}{b}=\frac{a.\left(-1\right)}{b.\left(-1\right)}=\frac{-a}{-b}\)
vì b < 0 => -b > 0
p\s : -b ko phải âm b mà là số đối của b
số nào nhân vs -1 cx = số đối của chính nó
Vận dụng kiến thức sau để giải thích
Khi đổi dấu cả tử số và mẫu số của một phân số ta được một phân số mới bằng phân số đã cho
Ta có thể viết một phân số bất kì có mẫu âm thành phân số bằng nó có mẫu dương bằng cách nhân cả tử và mẫu của phân số đó với -1
\(\frac{a}{b}\)= \(\frac{-a}{-b}\)