Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

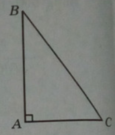
Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
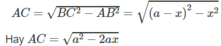
Diện tích tam giác ABC là:
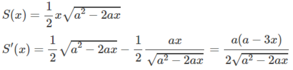
S′(x) = 0 ⇔ x = a/3
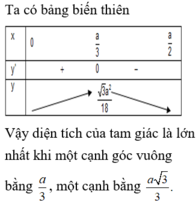
Bảng biến thiên:
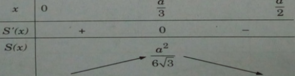
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3

Gọi cạnh góc vuông là \(x\) thì cạnh huyền là \(a-x\) (điều kiện: \(0< x< a-x\Leftrightarrow0< x< \dfrac{a}{2}\)) và cạnh góc vuông kia là: \(\sqrt{\left(a-x\right)^2-x^2}\).
Diện tích tam giác vuông là:
\(S=\dfrac{1}{2}x\sqrt{\left(a-x\right)^2-x^2}=\dfrac{1}{2}x\sqrt{a^2-2ax}\)
\(S'=\dfrac{1}{2}\sqrt{a^2-2ax}+\dfrac{1}{2}x\dfrac{-a}{\sqrt{a^2-2ax}}\)
\(=\dfrac{1}{2}\dfrac{a^2-3ax}{\sqrt{a^2-2ax}}\)
\(S'=0\Leftrightarrow x=\dfrac{a}{3}\)
S' đổi dấu từ dương sang âm khi x đi qua điểm \(\dfrac{a}{3}\) nên S đạt cực đại tại \(x=\dfrac{a}{3}\).
Khi đó diện tích tam giác vuông là:
\(S\left(\dfrac{a}{3}\right)=\dfrac{1}{2}\dfrac{a}{3}\sqrt{a^2-2a.\dfrac{a}{3}}=\dfrac{a^2\sqrt{3}}{18}\)

Cạnh đó là:
66,3 x 2 : 3,4=39( m )
Cạnh kia là:
88 - 39= 49 ( m )
Diện tích đất bạn đầulà:
39 x 49 = 1911 ( m2)
Đ/s: 1911 m2
~ Hok t ~

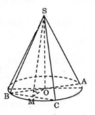
Ta có thiết diện qua trục của hình nón là tam giác vuông cân SAb, cạnh huyền A B = a 2
Vậy đường cao, bán kính và đường sinh của hình nón là:
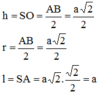
Diện tích xung quanh và diện tích toàn phần của hình nón là:
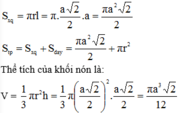
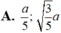
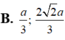
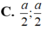
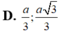




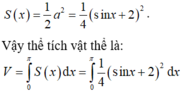
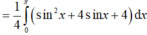
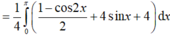
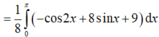

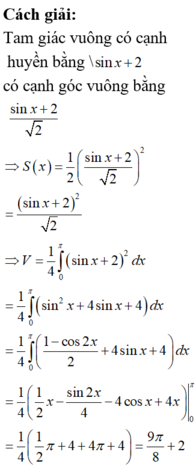
Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
Diện tích tam giác ABC là:
S′(x) = 0 ⇔ x = a/3
Bảng biến thiên:
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3.