Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=(-3;5] hợp [8;10] hợp [2;8)
=(-3;5) hợp [2;8) hợp [8;10]
=(-3;8) hợp [8;10]
=(-3;10]
B=[0;2] hợp (-vô cực;5] hợp (1;+vô cực)
=(-vô cực;5] hợp (1;+vô cực)
=(-vô cực;+vô cực)=R
C=[-4;7] hợp (0;10)
Vì (0;7] thuộc (0;10) nên [-4;7] hợp (0;10)=[-4;10)
D=(-vô cực;3] hợp (-5;+vô cực)
=(-5;3]
E=(3;+vô cực)\(-vô cực;1]
=(3;+vô cực)(Vì ko có phần tử nào có trong (3;+vô cực) nằm trong(-vô cực;1])
F=(1;3]\[0;4)=rỗng(Bởi vì (1;3] là tập con của [0;4))

Tham khảo:
a) Ta có:
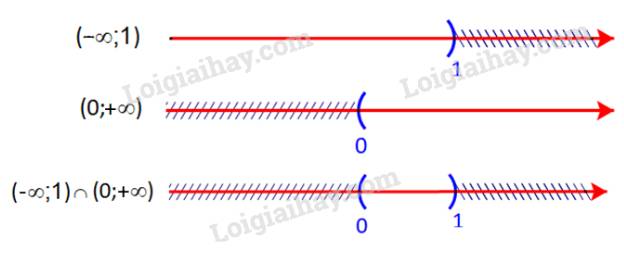
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:

Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
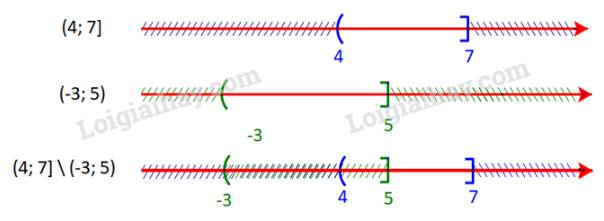
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)

a, \(A\cup B=(-4;5]\)
\(A\cap B=[-3;4)\)
\(A\backslash B=\left[4;5\right]\)
\(B\backslash A=\left(-4;-3\right)\)
b, \(A\cup B=\left(-3;7\right)\)
\(A\cap B=[1;2)\cup(3;5]\)
\(A\backslash B=\left[2;3\right]\)
\(B\backslash A=\left(-3;1\right)\cup\left(5;7\right)\)
c, \(A\cup B=\left[\dfrac{1}{2};3\right]\)
\(A\cap B=\left[1;\dfrac{3}{2}\right]\)
\(A\backslash B=[\dfrac{1}{2};1)\)
\(B\backslash A=(\dfrac{3}{2};3]\)
d, \(A\cup B=(-5;2]\cup(3;6]\)
\(A\cap B=\left\{0\right\}\cup[4;5)\)
\(A\backslash B=(0;2]\cup\left[-5;6\right]\)
\(B\backslash A=[-5;0)\cup\left(3;4\right)\)

f.
\(x+1>0\) và \(7-2x>0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>-1\\x< \dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow\) TXĐ: \(D=(-1;\dfrac{7}{2})\)
g.
\(x+1>0\) và \(x^2-4\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>-1\\x\ne2\\x\ne-2\end{matrix}\right.\)
\(\Rightarrow\) TXĐ: \(D=\left(-1;+\infty\right)\backslash2\)
h: ĐKXĐ: |x+1|-|x-2|<>0
=>|x+1|<>|x-2|
=>x-2<>x+1 và x+1<>-x+2
=>2x<>1
=>x<>1/2
g: ĐKXĐ: x+1>0 và x+2>=0 và x^2-4<>0
=>x>-2 và x>-1 và x<>2; x<>-2
=>x>-1; x<>2
f: ĐKXĐ: x+1>=0 và 7-2x>=0 và x+1<>7-2x
=>3x<>6 và -1<=x<=7/2
=>x<>2 và -1<=x<=7/2

Câu 1:
\(\Delta=m^2-4\left(m+3\right)\le0\)
\(\Leftrightarrow m^2-4m-12\le0\Rightarrow-2\le m\le6\)
Câu 2:
Để BPT đã cho vô nghiệm tương đương \(mx^2-4\left(m+1\right)x+m-5\le0\) đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\3m^2+13m+4\le0\end{matrix}\right.\) \(\Leftrightarrow-4\le m\le-\frac{1}{3}\)
Tất cả các đáp án đều sai
Câu 3:
Để pt có 2 nghiệm pb
\(\Leftrightarrow\Delta'=\left(m-2\right)^2+2\left(m-2\right)>0\)
\(\Leftrightarrow m^2-2m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\)
Tiếp tục tất cả các đáp án đều sai, đề bài gì kì vậy ta

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)
\(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)
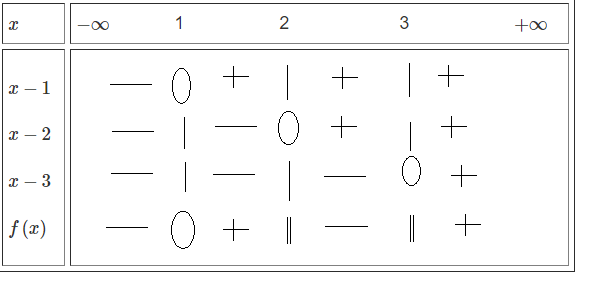
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)
\(\Rightarrow B.\)
TXĐ:`{(7-x>=0),(4x^2-19x+12>0):}`
`<=>{(x<=7),((x-4)(4x-3)>0):}`
`<=>{(x<=7),([(x>4),(x<3/4):}):}`
`=>[(x<3/4),(4<x<=7):}`
`=>D(-oo,3/4) UU (4;7]`