Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=sin\left(x-\dfrac{\pi}{2}\right)=-sin\left(\dfrac{\pi}{2}-x\right)=-cosx\)
\(y\left(-x\right)=-cos\left(-x\right)=-cosx=y\left(x\right)\)
Hàm đã cho là hàm chẵn

a) Ta có:
- Hàm số y = cos 3x có tập xác định là D = R
- ∀ x ∈ D ⇒ - x ∈ D
- và f(-x) = cos 3(-x) = cos (-3x) = cos(3x) = f(x)
Vậy hàm số y = cos 3x là hàm số chẵn
b)
Ta có:
Hàm số \(y=tan\left(x+\dfrac{\pi}{5}\right)\) không là hàm số lẻ vì:
\(y=tan\left(x+\dfrac{\pi}{5}\right)\) có tập xác định là \(D=R\backslash\left\{\dfrac{3\pi}{10}+k\pi\right\}\).
Mà với mọi x ∈ D, ta không suy ra được -x ∈ D
Chẳng hạn:
Lấy \(x=-\dfrac{3\pi}{10}\in D\). Ta có \(-x=\dfrac{3\pi}{10}\notin D\).
Vậy hàm số \(y\left(x\right)\) có tập xác định không tự đối xứng nên \(y=tan\left(x+\dfrac{\pi}{5}\right)\) không là hàm số lẻ.

a. y = f(x) = cos3x là hàm số chẵn vì:
+ TXĐ: D = R ⇒ ∀ x ∈ D ta có: - x ∈ D
+ f(-x) = cos3.(-x) = cos(-3x) = cos 3x = f(x) ∀ x ∈ D

a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | \(0\) | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | 0 | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 |
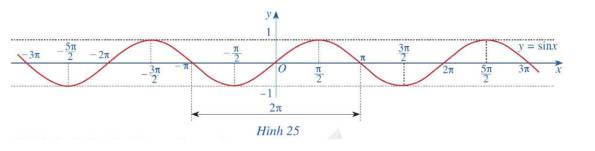
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)

a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)

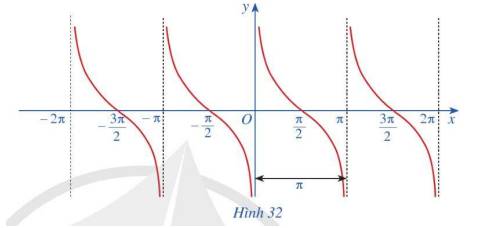
a) Tập giá trị của hàm số \(y = \cot x\)là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Hàm số \(y = \cot x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\)
Hàm số \(y = \cot x\) có tuần hoàn
d) Hàm số \(y = \cot x\)nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\)

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \tan x\) là hàm số lẻ.
b)
\(x\) | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | \( - \frac{\pi }{6}\) | \(0\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | \( - \sqrt 3 \) | \( - 1\) | \( - \frac{{\sqrt 3 }}{3}\) | \(0\) | \(\frac{{\sqrt 3 }}{3}\) | \(1\) | \(\sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).


Xét hàm số y= f(x) = 10.sinx. cos3x
TXĐ: D= R.
∀ x ∈ D ⇒ - x ∈ D và f (-x) = 10. sin(-x). cos3 ( -x) = 10.(- sinx). cosx= - f(x)
Do đó, hàm số y = 10sinx. cos3x là hàm số lẻ R.
Đáp án B