

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Tại vị trí cân bằng của hệ hai vật ta có

![]()
Khi đốt dây, hợp lực tác dụng lên vật A lúc này là:
![]()
Lực này gây ra cho vật A gia tốc 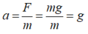
Vì vật đang ở vị trí biên nên a chính là gia tốc cực đại
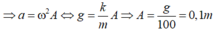
Mà vật A đi từ vị trí thấp nhất đến vị trí cao nhất mất nửa chu kì nên
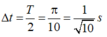
Cũng trong khoảng thời gian ∆ t ấy vật B rơi tự do được quãng đường:
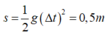
Vậy khoảng cách giữa A và B lúc này là: 2A+1+s=80 cm.

Đáp án B
+ Sau khi vật B tách rời, vật A dao động với chu kì
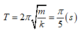
và biên độ 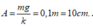
Khi A lên đến điểm cao nhất thì đi được quãng đường
![]()
trong thời gian 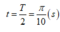
+ Trong khoảng thời gian t = π/10 (s) vật B rơi tự do được quãng đường
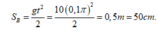
→ khoảng cách giữa hai vật là
![]()

Theo bài ra ta có
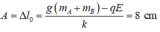
Khi dây bị đứt vật A dao động với biên độ A1, chu kỳ T1 và có VTCB là Om cao hơn VTCB cũ một đoạn
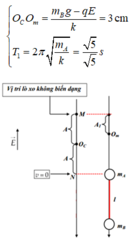
Vật B rơi tự do với gia tốc g1. Trong khoảng thời gian từ khi vật đi từ khi tuột dây đến khi vật A lên đến vị trí cân bằng Om là t = T 1 4 thì vật B đi được quãng đường là s1

Đáp án B

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng O của hệ hai vật Δ l 0 = 2 m g k = 5 cm, kéo hệ xuống dưới vị trí cân bằng 10 cm rồi thả nhẹ, vậy hệ sẽ dao động với biên độ A = 10 cm.
+ Ta có thể chia quá trình chuyển động của hệ thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật dao động điều hòa quanh vị trí cân bằng O.
· Tốc độ của hai vật khi đi qua vị trí cân bằng v m a x = ω A = k 2 m A = 100 2 cm/s.
Giai đoạn 2: Chuyển động của hai vật sau khi đi qua vị trí cân bằng O.
· Khi đi qua vị trí cân bằng O, tốc độ của vật A sẽ giảm, vật B sẽ chuyển động thẳng đứng lên trên với vận tốc ban đầu bằng v m a x , do có sự khác nhau về tốc độ nên hai vật không dao động chung với nhau nữa.
· Tuy nhiên sự kiện trên chỉ diễn ra rất ngắn, vật A ngay sau đó sẽ dao động quanh vị trí cân bằng mới ở phía trên O một đoạn 2,5 cm do đó ngay lập tức tốc độ của A sẽ tăng, trong khi B lại giảm → hệ hai vật lại được xem như ban đầu và dao động quanh vị trí cân bằng O.
Giai đoạn 3: Chuyển động của hai vật sau khi dây bị chùng
· Phương trình định luật II cho vật m 2 : m 2 g − T = m 2 a , khi T = 0 dây chùng → x = − g ω 2 = − 5 cm. Lúc này v A = 3 2 v m a x = 50 6 cm/s.
· Vật dao A dao động quanh vị trí cân bằng mới O' cách vị trí cân bằng cũ một đoạn Δ l = m g k = 2 , 5 cm với biên độ A ' = 2 , 5 2 + 50 6 20 2 = 6 , 61 cm.
Từ các lập luận trên ta thấy rằng khi A dừng lại lần đầu tiên ứng với vị trí biên trên, khi đó quãng đường vật đi được sẽ là S = 10 + 5 + (6,61 – 2,5) = 19,1 cm.

Chọn B
+ Sau khi cắt sợi dây, con lắc mới gồm lò xo và vật M có vị trí cân bằng mới O1 cách vị trí cân bằng của con lắc cũ O gồm lò xo và vật M+m một đoạn bằng độ giãn của lò xo do vật m gây ra.
+ Việc cắt sợi dây làm cho vật M dao động tương tự như cách kích thích dao động cho vật M bằng cách từ vị trí cân bằng O1 kéo vật M theo phương thẳng đứng xuống dưới tới vị trí O rồi thả nhẹ nên O1O bằng biên độ dao động của con lắc mới.
=> A = O1O = mg/k.

Đáp án C
![]() (Khi cắt đứt dây) =>A=10 cm
(Khi cắt đứt dây) =>A=10 cm
Xét ở thời điểm cắt dây đến khi vật lên đến vị trí cao nhất, vật 1 đi được quãng đường S1=20cm
Khi cắt dây thì vật 1 dao động với
![]()
Quảng đường vật 2 rơi tụ do trong T/2 (s) là:
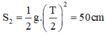
=> Khoảng cách giữa hai vật là:
![]()