Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

a) Trong tứ giác AOBM có 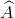 =
= 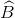 =
= 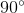 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 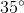
= 
b) Từ 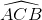 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 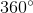 -
-  =
= 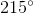

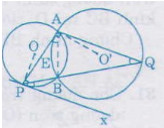
Ta có: 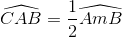 (1)
(1)
( vì 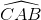 là góc tạo bởi một tiếp tuyến và một dây cung đi qua tiếp điểm A của (O')).
là góc tạo bởi một tiếp tuyến và một dây cung đi qua tiếp điểm A của (O')).
và 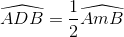 (2)
(2)
góc nội tiếp của đường tròn (O') chắn cung 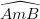
Từ (1), (2) suy ra
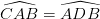 (3)
(3)
Chứng minh tương tự với đường tròn (O), ta có:
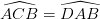 (4)
(4)
Hai tam giác ABD và ABC thỏa (3), (4) suy ra cặp góc thứ 3 của chúng bằng nhau, vậy 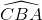 =
= 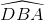

ME^2=MP*MK
=>ME/MK=MP/ME
=>ΔMEK đồng dạng vơi ΔMPE
=>góc MKE=góc PEM
=>góc KEF=góc KPE
góc KAB=góc KFB+góc KEF
=>gócKAF=góc KEF
=>KAEF nội tiếp
=>góc KFE+góc KAE=180 độ
mà góc KQC+góc KAC=180 độ
góc KQF+góc NFK=180 độ
nên góc KQF+góc NFQ+góc QFK=180 độ
màgóc KQF+góc QFK+góc QKF=180 độ
nên góc NFQ=góc QKF
góc NBK=1/2*sđ cung NK=góc KAF=góc AEF
=>NBEK nội tiếp
=>góc NKE+góc NBE=180 độ
góc NFK+góc FKE=góc NKE=180 độ-góc NBE
=>góc NKF=180 độ-góc NBE-góc FKE
=>góc NKF=180 độ-góc BCP-góc FAE
=>góc NKF=góc BAP-góc FAE=góc CAP
mà góc CAP=góc CBP=goc CFE=góc QFN=góc QKF
nên Q,K,N thẳng hàng

a) Ta có 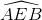 là góc có đỉnh ở bên ngoài đường tròn nên:
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy 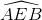 =
=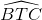
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)
Chon A