Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
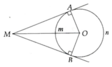
a, Chứng minh được OM là tia phân giác của góc
A
M
B
^
. Từ đó ta tìm được
A
M
O
^
=
20
0
và
A
O
M
^
=
70
0
b, sđ A m B ⏜ = A O B ^ = 140 0
=> sđ A n B ⏜ = 220 0
Bài 7:
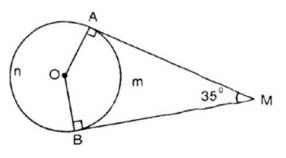
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)
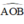
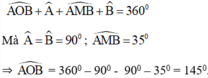
a) Trong tứ giác AOBM có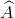
= 
= 
.
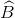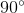Suy ra cung AMB +
= 
=> cung AMB=
- 
=
- 
=
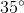
b) Từ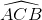
= 
. Suy ra số đo cung nhỏ AB = 
và số đo cung lớn AB :
Cung AB =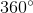
- 
= 