Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

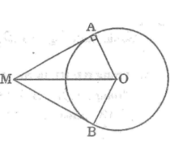
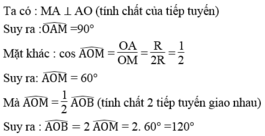
Xét ΔAOM vuông tại A có \(\cos\widehat{OAM}=\dfrac{R}{2R}=\dfrac{1}{2}\)
nên \(\widehat{OAM}=60^0\)(1)
Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: OM là phân giác của góc AOB(2)
Từ (1) và (2) suy ra \(\widehat{AOB}=120^0\)


a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE
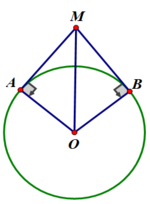
Đáp án A.120o
Tham khảo cách giải thích :