Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

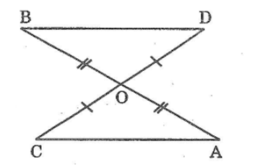
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)

b: Xét tứ giác ADBC có
O là trung điểm của AB
O là trung điểm của CD
Do đó: ADBC là hình bình hành
SUy ra: AC//BD

Xét tứ giác AMED có
AM//ED
EM//AD
Do đó: AMED là hình bình hành
Suy ra: AE và MD cắt nhau tại trung điểm của mỗi đường

TRẢ LỜI:
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Xét Δ AOC và Δ BOD có:
OA = OB (gt)
AOC = BOD (đối đỉnh)
OC = OD (gt)
Do đó, Δ AOC = Δ BOD (c.g.c)
=> ACO = ODB (2 góc tương ứng)
Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)

Cách 1:Xét tứ giác ADBC có
AB và CD cắt nhau tại O là trung điểm của mỗi đường
=>ADBC là hình bình hành
=>AC//BD(đl)
Cách 2 Chứng minh được \(\Delta AOC=\Delta BOD\left(AO=OC;\widehat{AOC}=\widehat{BOD};OC=OD\right)\)
\(\Rightarrow\widehat{CAO}=\widehat{DBO}\)Hay \(\widehat{CAB}=\widehat{DBA}\)
Hai góc này ở vị trí so le trong bằng nhau
=> AC//BD

Nối Avs C, C vs B, B vs D, D vs A
Gọi giao điểm của AB và CD là O
Xét tam giác AOC và tam giác BODcó:
AO=BO(gt)
goác AOC= goác BOD( đối đỉnh )
OC=OD(gt)
=> 2 tam giác trên bằng nhau
=>góc ACO=góc BDO ( 2 góc tương ứng )
Vì 2 góc trên nằm ở vị trí so le trong
=> AC song song với BD
=> DPCM