
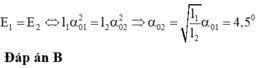
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

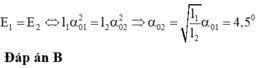

\(T_1=2\pi\sqrt{\dfrac{l_1}{g}}\left(1\right),T_2=2\pi\sqrt{\dfrac{l_2}{g}}\left(2\right)\)
\(T=2\pi\sqrt{\dfrac{l_1-l_2}{g}}\left(3\right)\)
Thay (1),(2) vào (3) ta được:
\(T=\sqrt{T_1^2-T_2^2}=1.5s\) ->C

Đáp án B
Phương pháp: Sử dụng công thức tính chu kì con lắc đơn
Cách giải :
Chu kì dao của con lắc đơn:
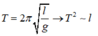
Khi con lắc có chiều dài l1 thì T12 ~ l1 ; khi con lắc có chiều dài l2 thì T2 2 ~ l2
Do đó khi con lắc có chiều dài l thì T 2 ~ l
Mà l = l1 + l2 → T2 = T12 + T22 = 0,62 + 0,82 = 1→ T = 1s
Chú ý: Nếu l = l1 + l2 thì T2 = T12 – T22

Áp dụng công thức tính năng lượng dao động của con lắc đơn ta có:
\(W_1 = \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}\) và \(W_2 = \dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Theo giả thiết hai con lắc đơn có cùng năng lượng
\(\Rightarrow \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}=\dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Do khối lượng hai con lắc bằng nhau nên:
\(\ell_1.\alpha_1 ^{2} = \ell_2. \alpha_2 ^{2}\)
\(\Rightarrow \alpha_2 = \alpha_1 .\sqrt{l1/l2}\).
Thay số ta tìm được: \(\alpha_2 = 5,625^0\)

Chọn đáp án A.
F 1 F 2 = P sin α 01 P sin α 02 ≈ S 01 l 1 S 02 l 2 = S 01 S 02 . l 2 l 1 = 1 2 . 2 3 = 1 3

Đáp án D
+ Ta có E A = E B ⇔ l A α A 2 = l B α B 2 → α B = α A l A l B = 2 , 7 0