Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{W_a}{W_b}=\dfrac{\dfrac{1}{2}m.v_1max^2}{\dfrac{1}{2}m.v_2max^2}=\dfrac{g.l_1.\alpha o1^2}{g.l_2.\alpha o^2}\)
dao động nhỏ nên anpha xấp xỉ sin anpha
B là 2
A là 1
tỉ số cơ năng là....

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Khi vật qua VTCB thì động năng bằng cơ năng, nếu giữ dây treo tại 1 vị trí nào đó thì tốc độ của vật không đổi --> động năng không đổi
--> Cơ năng không thay đổi.
Chọn phương án B.

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)

Áp dụng công thức tính năng lượng dao động của con lắc đơn ta có:
\(W_1 = \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}\) và \(W_2 = \dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Theo giả thiết hai con lắc đơn có cùng năng lượng
\(\Rightarrow \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}=\dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Do khối lượng hai con lắc bằng nhau nên:
\(\ell_1.\alpha_1 ^{2} = \ell_2. \alpha_2 ^{2}\)
\(\Rightarrow \alpha_2 = \alpha_1 .\sqrt{l1/l2}\).
Thay số ta tìm được: \(\alpha_2 = 5,625^0\)

Sau đây là keys
1/ \(A.T=2\pi\sqrt{\dfrac{m}{k}}\)
2/ \(D.\) Cộng hưởng cơ
3/ \(\varphi_1-\varphi_2=\pi+2k\pi=\left(2k+1\right)\pi\Rightarrow A.\left(2k+1\right)\pi\)
4/ \(\omega=2\pi f\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{\pi}{2\pi}=\dfrac{1}{2}\left(Hz\right)\Rightarrow A.0,5Hz\)
5/ \(A.\) Cơ năng, biên độ, tần số
6/ Câu này vẽ đường tròn ra là xong thôi
\(\varphi=arc\cos\left(\dfrac{3}{6}\right)+\dfrac{\pi}{2}+arc\sin\left(\dfrac{3\sqrt{3}}{6}\right)=\dfrac{\pi}{3}+\dfrac{\pi}{2}+\dfrac{\pi}{3}=\dfrac{7\pi}{6}\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{7\pi}{6.4\pi}=\dfrac{7}{24}\left(s\right)\Rightarrow A.\dfrac{7}{24}\left(s\right)\)
7/ \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}k\dfrac{4}{9}A^2\Rightarrow\dfrac{W_t}{W}=\dfrac{\dfrac{2}{9}kA^2}{\dfrac{1}{2}kA^2}=\dfrac{4}{9}\Leftrightarrow W_t=\dfrac{4}{9}W\left(J\right)\)
\(\Rightarrow W_d=W-W_t=W-\dfrac{4}{9}W=\dfrac{5}{9}W\left(J\right)\Rightarrow B.\dfrac{5}{9}W\left(J\right)\)
Câu này em nghĩ nên cho thêm đơn vị Jun ạ!
8/ \(T-mg\cos\alpha=m.a_{ht}=\dfrac{mv^2}{l}\)
\(\Leftrightarrow T=mg\cos\alpha+2mg\left(\cos\alpha-\cos\alpha_0\right)\)
\(\Leftrightarrow T=mg\left(3\cos\alpha-2\cos\alpha_0\right)\)
Lực căng cực đại khi vật ở vị trí thấp nhất
\(\Rightarrow\alpha=0\Rightarrow T_{max}=mg\left(3.1-2\cos60^0\right)=2mg\left(N\right)\)
Lực căng cực tiểu khi vật ở vị trí ban đầu
\(\Rightarrow\alpha=60^0\Rightarrow T_{min}=mg\left(3.\dfrac{1}{2}-2.\dfrac{1}{2}\right)=0,5mg\left(N\right)\)
\(\Rightarrow\dfrac{T_{max}}{T_{min}}=\dfrac{2}{0,5}=4\Rightarrow D.4\)
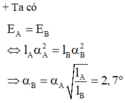



Đáp án D
+ Ta có E A = E B ⇔ l A α A 2 = l B α B 2 → α B = α A l A l B = 2 , 7 0