Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(A_7^3-A_6^2=180\) số
Các trường hợp số chữ số lẻ nhiều hơn số chữ số chẵn là: 3 chữ số đều lẻ, 2 chữ số lẻ 1 số chữ chẵn
- 3 chữ số đều lẻ: \(A_3^3=3\) số
- 2 chữ số lẻ 1 chữ số chẵn: chọn 2 chữ số lẻ từ 3 chữ số lẻ có \(C_3^2=3\) cách
+ Nếu chữ số chẵn là 0 \(\Rightarrow\) \(3!-2!=4\) cách hoán vị 3 chữ số
+ Nếu chữ số chẵn khác 0 \(\Rightarrow\) có 3 cách chọn chữ số chẵn và \(3!\) cách hoán vị các chữ số
\(\Rightarrow3+3.\left(4+3.3!\right)=69\) số
Xác suất: \(P=\dfrac{69}{180}=\dfrac{23}{60}\)

Tổng 5 chữ số bất kì luôn \(\ge0+1+2+3+4=10\) => Mọi chữ số đề \(\le8\)
Nếu X không có 0 tổng 5 chữ số bất kì luôn \(\ge1+2+3+4+5=15\) => Mọi chữ số đều \(\le3\) ---> Vô lý
Vậy X luôn có 0 và không có 9.
Các X bộ số thỏa mãn:
+) \(\left(0;1;2;3;4;8\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
+) \(\left(0;1;2;3;5;7\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 4.4! = 216 số chẵn
+) \(\left(0;1;2;4;5;6\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
=> Xác suất chọn được số chẵn: \(P=\dfrac{408+408+216}{600\cdot3}=\dfrac{43}{75}\)

Chọn B
Số phần tử của không gian mẫu ![]()
Gọi biến cố A” Chọn được một số thỏa mãn ![]() ”.
”.
Vì mà nên trong các chữ số sẽ không có số 0.
TH1: Số được chọn có chữ số giống nhau có 9 số.
TH2: Số được chọn tạo bới hai chữ số khác nhau.
Số cách chọn ra 2 chữ số khác nhau từ 9 chữ số trên là: C 9 2 .
Mỗi bộ 2 chữ số được chọn tạo ra 2 số thỏa mãn yêu cầu.
Vậy có 2. C 9 2 số thỏa mãn.
TH3: Số được chọn tạo bởi ba chữ số khác nhau.
Số cách chọn ra 3 chữ số khác nhau từ 9 chữ số trên là: C 9 3 .
Mỗi bộ 3 chữ số được chọn chỉ tạo ra một số thỏa mãn yêu cầu.
Vậy có C 9 3 số thỏa mãn.
Vậy ![]()
Xác suất của biến cố A là: .
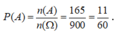

Chọn D
Gọi số có 6 chữ số có dạng ![]()
Từ 10 chữ số {0;1;2;3;4;5;6;7;8;9}, ta lập được 9. A 9 5 số có 6 chữ số đôi một khác nhau.
Lấy ngẫu nhiên một số từ tập X ![]()
Gọi A là biến cố “Lấy một số thuộc X luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ ”.
Ta coi 3 vị trí liền nhau trong X là một phần tử Z, sắp xếp 3 chữ số khác nhau trong Z thỏa mãn biến cố :
+ Số thứ nhất là số lẻ thuộc Y có 3 cách chọn.
+ Số thứ hai là số chẵn thuộc Y có 2 cách chọn.
+ Số thứ ba là số lẻ thuộc Y có 2 cách chọn.
Áp dụng quy tắc nhân ta có 12 cách sắp xếp phần tử .
Trường hợp 1: Số có 6 chữ số có dạng ![]()
+) z có 12 cách chọn.
+) Xếp 5 chữ số còn lại khác các số tập Y vào 3 vị trí ![]()
Áp dụng quy tắc nhân, ta lập được ![]()
Trường hợp2: Số có 6 chữ số có dạng ![]()
+)
a
1
có 4 cách chọn ![]()
+) Xếp z vào 3 vị trí, z có 12 cách chọn nên có 36 cách sắp xếp.
+) Xếp 4chữ số còn lại vào 2 vị trí ![]()
Áp dụng quy tắc nhân, ta lập được 4.36. A 4 2 = 1728 số có 6 chữ số đôi một khác nhau thỏa mãn.
Vậy ta có tất cả ![]() (số) thoả mãn yêu cầu bài toán.
(số) thoả mãn yêu cầu bài toán.
![]()

Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 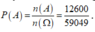
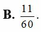
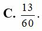

GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG