
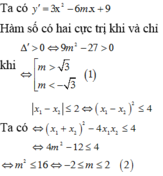

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

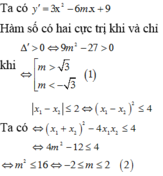


Chọn C.
+) Ta có ![]()
![]()
+) Theo giả thiết hàm số đạt cực trị tại ⇔ phương trình (1) có 2 nghiệm phân biệt
![]()
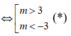
+) Với điều kiện (*) thì phương trình (1) có nghiệm x 1 , x 2 , theo Vi-ét ta có:
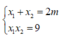
+) Ta lại có ![]()
![]()
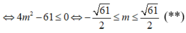
+) Kết hợp (*), (**) và điều kiện m dương ta được: 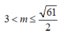


Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

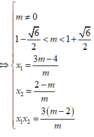

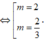

\(y=\dfrac{x^2+mx+1}{x+m}=x+\dfrac{1}{x+m}\)
\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}1-\dfrac{1}{\left(2+m\right)^2}=0\\\dfrac{2}{\left(m+2\right)^3}< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}m=-3\\m< -2\end{matrix}\right.\)
Chọn a