
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Ta có: \(\left|x+\dfrac{1}{7}\right|\ge0\forall x,\left|y-12\right|\ge0\forall y\)
\(\Rightarrow A=\left|x+\dfrac{1}{7}\right|+\left|y-12\right|\ge0\)
\(minA=0\Leftrightarrow\) \(\left\{{}\begin{matrix}x+\dfrac{1}{7}=0\\y-12=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{7}\\y=12\end{matrix}\right.\)
\(A=\left|x+\dfrac{1}{7}\right|+\left|y-12\right|\)
Vì \(\left\{{}\begin{matrix}\left|x+\dfrac{1}{7}\right|\text{≥}0\\\left|y-12\right|\text{≥}0\end{matrix}\right.\)
⇒\(\left|x+\dfrac{1}{7}\right|+\left|y-12\right|\text{≥}0\)
Min \(A=0\)⇔\(\left\{{}\begin{matrix}x+\dfrac{1}{7}=0\\y-12=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=-\dfrac{1}{7}\\y=12\end{matrix}\right.\)


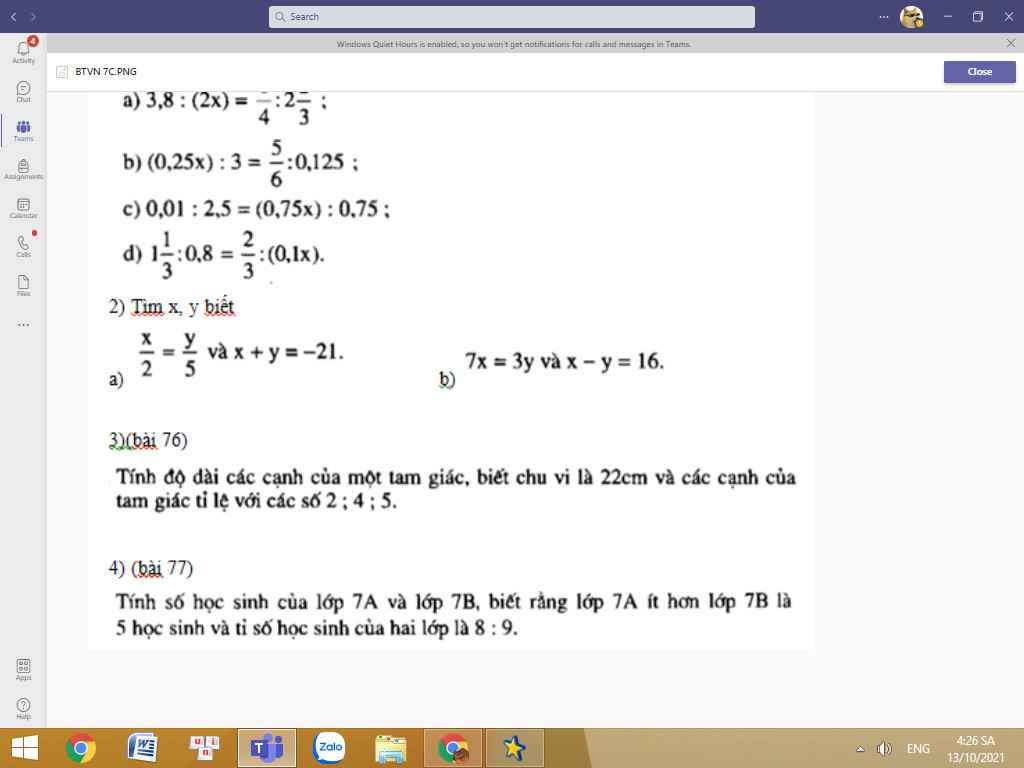
Bài 77:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-8}=5\)
Do đó: x=40; y=45

Câu 4:
Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|2y+3\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|2y+3\right|\ge0\forall x,y\)
Dấu '='xảy ra khi x=-2 và \(y=-\dfrac{3}{2}\)


Để Q(x) có nghiệm thì Q(x) = 0
Hay: \(2x^2-3x+1=0\)
\(\Rightarrow2x^2-2x-x+1=0\)
\(\Rightarrow2x\left(x-1\right)-\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy...
`2x^2-3x+1=0`
`<=>2x^2-x-2x+1=0`
`<=>x(2x-1)-(2x-1)=0`
`<=>(2x-1)(x-1)=0`
`<=>x=1\or\x=1/2`

`# \text {Kaizu DN}`
`a)`
`(3x + 6) + (7x - 14) = 0?`
\(\Rightarrow3x+6+7x-14=0\\ \Rightarrow\left(3x+7x\right)+\left(6-14\right)=0\\ \Rightarrow10x-8=0\\ \Rightarrow10x=8\Rightarrow x=\dfrac{8}{10}\\ \Rightarrow x=\dfrac{4}{5}\)
Vậy, \(x=\dfrac{4}{5}\)
`b)`
`17y + 35 + 4x + 17 = 42`
\(\Rightarrow\left(17y+17\right)+\left(35+4x\right)=42\\ \Rightarrow17\left(y+1\right)+\left(35+4x\right)=42\)
Bạn xem lại đề ;-;.

5: \(=\dfrac{1}{2}\cdot10-\dfrac{1}{2}=\dfrac{1}{2}\cdot9=\dfrac{9}{2}\)


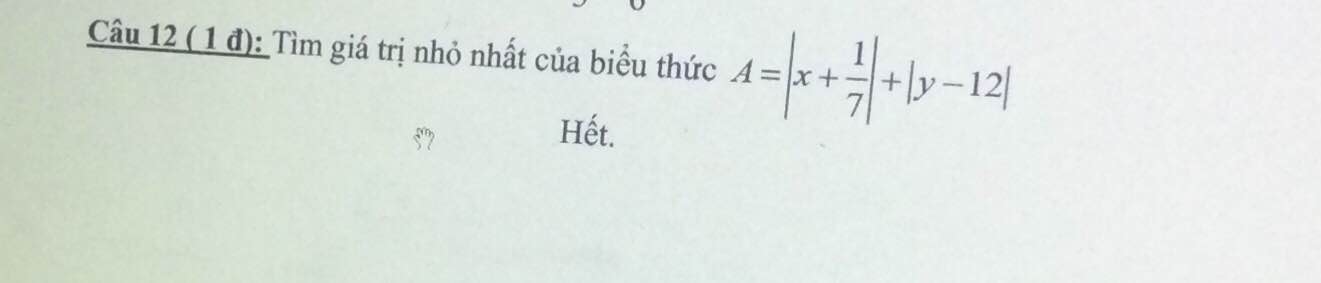

 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ
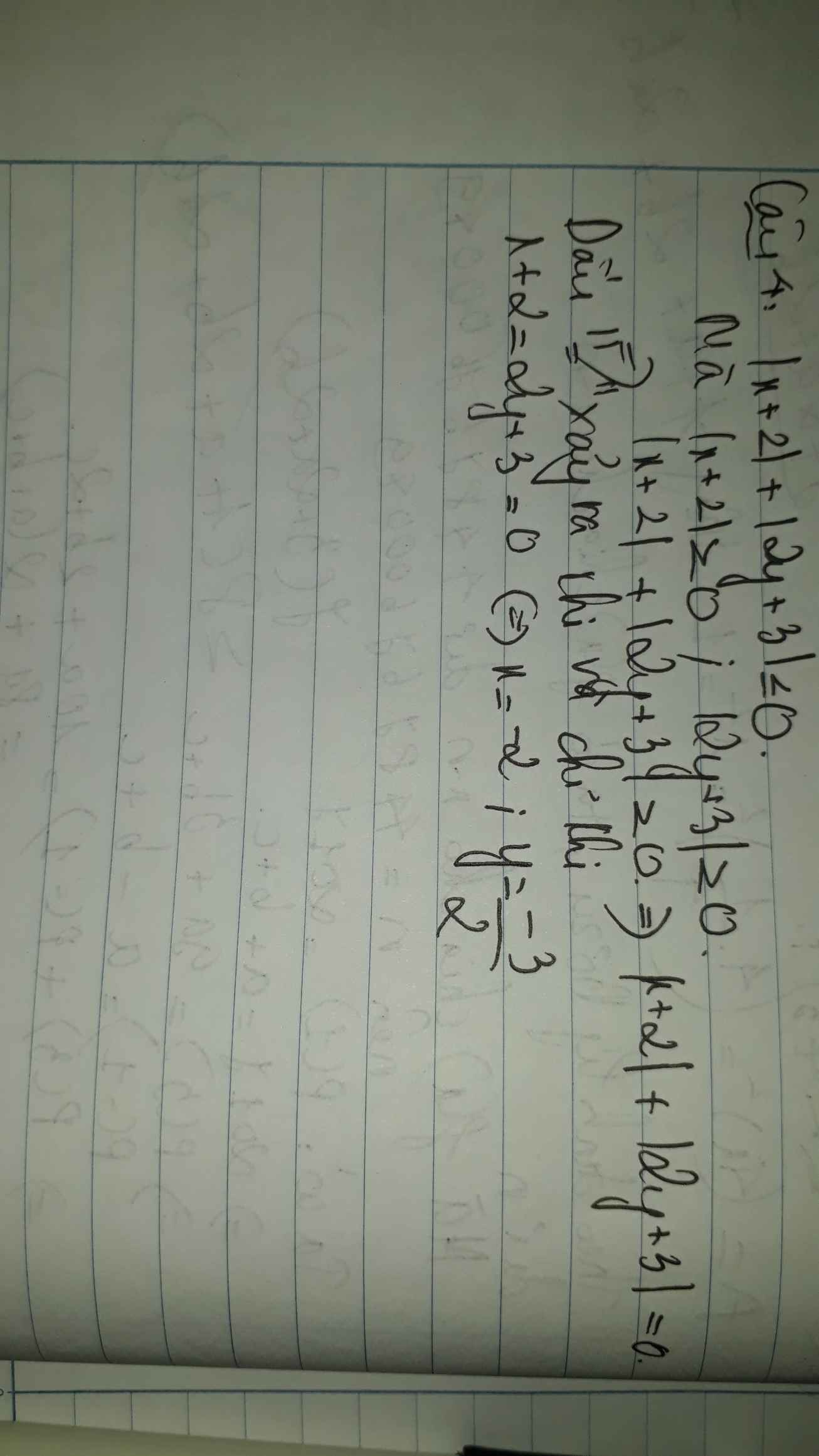
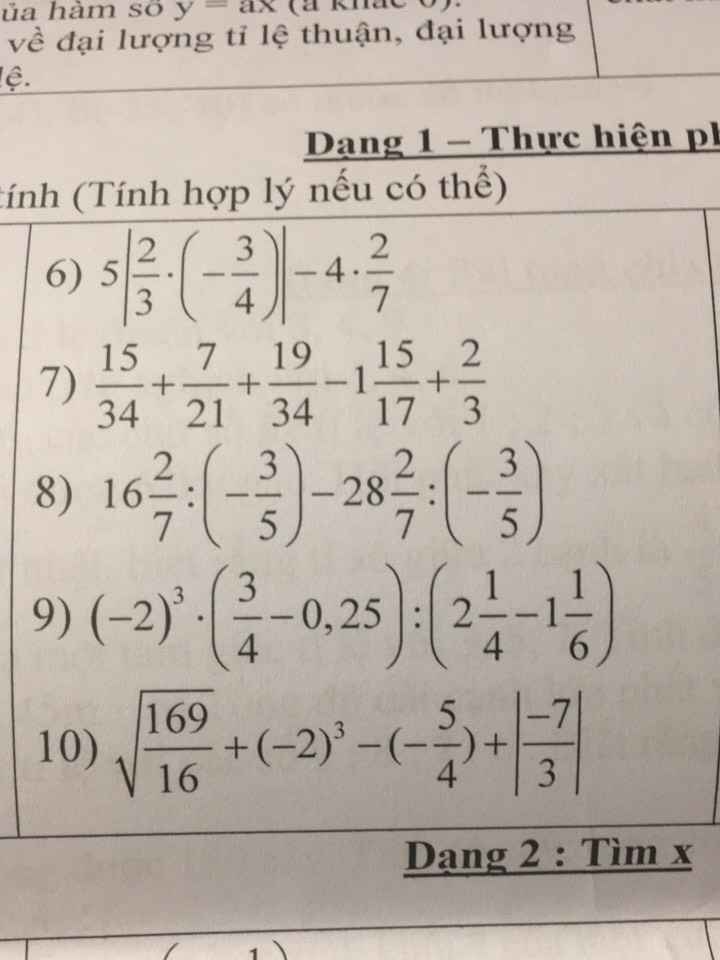
Câu 1:
\(A=10\sqrt{0,01}-\sqrt{\dfrac{9}{16}}+3\sqrt{49}-\dfrac{1}{6}\sqrt{4}\)
\(=10.\dfrac{1}{10}-\dfrac{3}{4}+3.7-\dfrac{1}{6}.2\)
\(=1-\dfrac{3}{4}+21-\dfrac{1}{3}=\dfrac{251}{12}\)
Câu 2:
Do \(\left|x+2\right|,\left|2y+3\right|\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}x+2=0\\2y+3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=-\dfrac{3}{2}\end{matrix}\right.\)