Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$4x-6=2x+4$
$\Leftrightarrow (4x-6)-(2x+4)=0$
$\Leftrightarrow 2x-10=0$
$\Leftrightarrow 2x=10$
$\Leftrightarrow x=5$

b: Ta có: \(\left(x-4\right)^2-x\left(x+1\right)\)
\(=x^2-8x+16-x^2-x\)
=-9x+16

x^3-6x^2+12x-8=0
-> x^3-2x^2-4x^2+8x+4x-8=0
-> x^2(x-2)-4x(x-2)+4(x-2)=0
-> (x-2)(x^2-4x+4)=0
->(x-2)(x-2)^2=0
-> (x-2)^3=0
->x-2=0
-> x=2 .
x^3-6x^2+12x-8=0
-> x^3-2x^2-4x^2+8x+4x-8=0
-> x^2(x-2)-4x(x-2)+4(x-2)=0
-> (x-2)(x^2-4x+4)=0
->(x-2)(x-2)^2=0
-> (x-2)^3=0
->x-2=0
-> x=2 .
nha ><

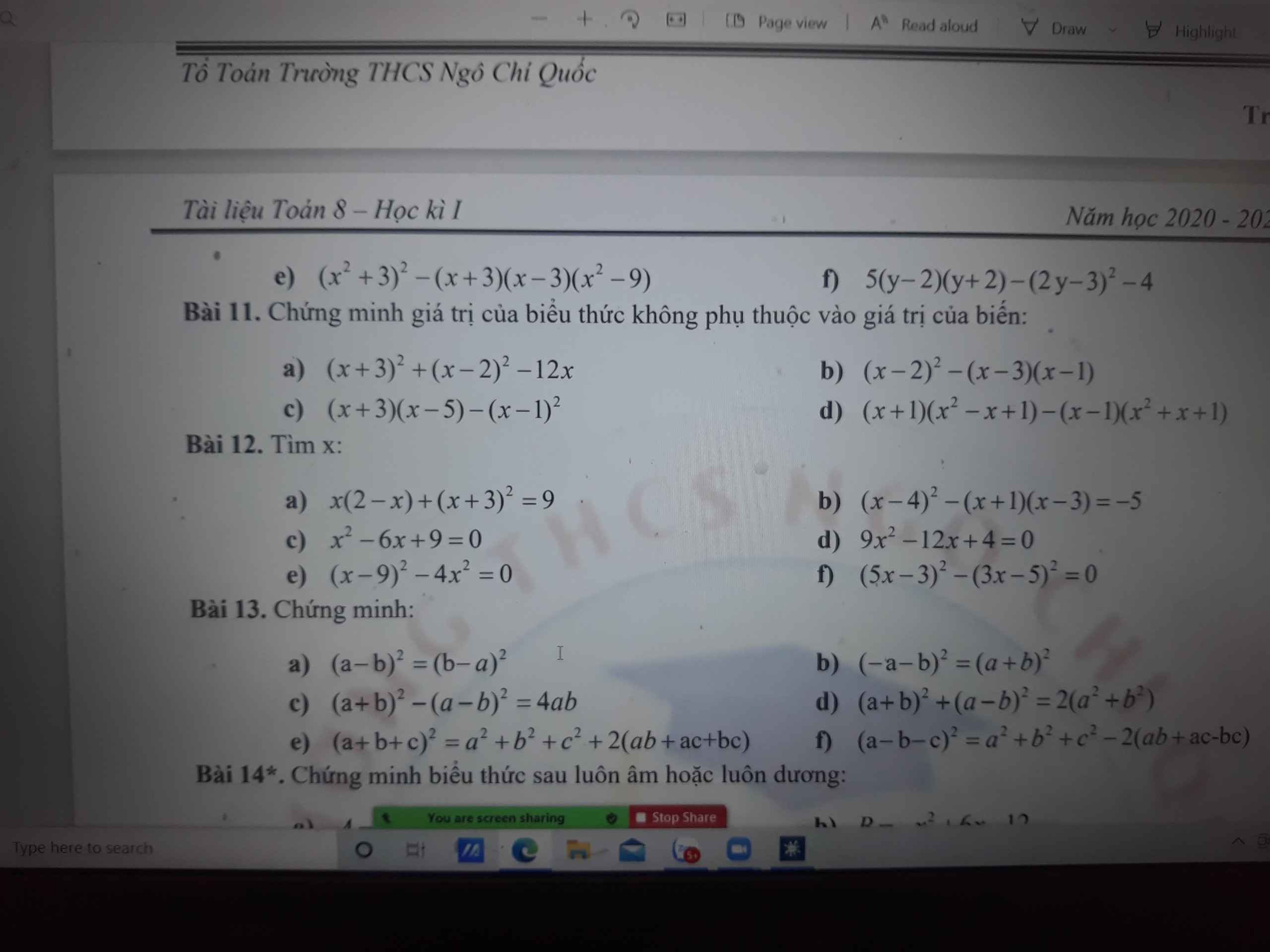
(x + 8)2 - x(x + 6) = 34
<=> x2 + 16x + 64 - x2 - 6x = 34
<=> 10x = - 30
<=> x = - 3

\(3x^2+x+11=0\)
\(x^2+x+\frac{1}{4}+2x^2+\frac{43}{4}=0\)
\(\left(x+\frac{1}{2}\right)^2+2x^2+\frac{43}{4}=0\)
Mà \(\left(x+\frac{1}{2}\right)^2+2x^2+\frac{43}{4}\ge\frac{43}{4}\forall x\)
=> PT vô nghiêm
\(3x^2+x+11=0\)
\(\Leftrightarrow x^2+\frac{1}{3}x+\frac{11}{3}=0\)
\(\Leftrightarrow x^2+2\frac{1}{3}.\frac{1}{2}x+\frac{1}{36}+\frac{131}{36}=0\)
\(\Leftrightarrow\left(x+\frac{1}{6}\right)^2=-\frac{131}{36}\left(voly\right)\)
=> Phương Trình Vô Nghiệm

b) \(\left(3x-9\right)\times12=36\)
\(3x-9=36\div12=3\)
\(3x=3+9=12\)
\(x=12\div3\)
\(x=4\)
c) \(\left(x+1\right)+\left(x+4\right)+...+\left(x+100\right)=1751\)
\(x+1+x+4+....+x+100=1751\)
\(\left(x+x+...+x\right)+\left(1+4+...+100\right)=1751\)
Số số hạng là \(\left(100-1\right)\div3+1=34\) ( số hạng )
=> Ta có 34 số hạng x
Tổng là \(\left(100+1\right)\times34\div2=1717\)
=> \(x\times34+1717=1751\)
\(x\times34=1751-1717\)
\(x\times34=34\)
\(x=34\div34\)
\(x=1\)
b; (3\(x\) - 9).12 = 36
3\(x\) - 9 = 36: 12
3\(x\) - 9 = 3
3\(x\) = 3 + 9
3\(x\) = 12
\(x\) = 12: 3
\(x\) = 4
c, (\(x\) + 1) + (\(x\) + 4)+...+ (\(x\) + 100) = 1751
Dãy số trên là dãy số cách đều với khoảng cách là:
\(x\) + 4 - \(x\) - 1 = 3
Số số hạng của dãy số trên là:( \(x\) + 100 - \(x\) - 1):3 = 34
Ta có: (\(x\) + 100 + \(x\) + 1)\(\times\) 34 : 2 = 1751
(2\(x\) + 101) \(\times\) 17 = 1751
2\(x\) + 101 = 1751 : 17
2\(x\) + 101 = 103
2\(x\) = 103 - 101
2\(x\) = 2
\(x\) = 1

\(x^2-14x+13=0\)
\(\Rightarrow x^2-2x.7+7^2-7^2+13=0\)
\(\Rightarrow\left(x^2-2x.7+7^2\right)-7^2+13=0\)
\(\Rightarrow\left(x-7\right)^2-49+13=0\)
\(\Rightarrow\left(x-7\right)^2-36=0\)
\(\Rightarrow\left(x-7\right)^2=36\)
\(\Rightarrow\left(x-7\right)^2=\pm6^2\)
\(\Rightarrow\orbr{\begin{cases}x-7=6\\x-7=-6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=13\\x=1\end{cases}}\)
Vậy ...
\(x^2-14x+13=0\)
\(x^2-14x+49-36=0\)
\(\left(x^2-14x+19\right)-36=0\)
\(\left(x-7\right)^2-6^2=0\)
\(\left(x-7-6\right)\left(x-7+6\right)=0\)
\(\left(x-13\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-13=0\\x-1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=13\\x=1\end{cases}}\)