Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt OA = x và OB =y, ta có:
S A B C D = 1 2 A C . B D = 1 2 2 x .2 y = 2 x y
Theo giả thiết, ta có: 2 ( x + y ) = 46 x 2 + y 2 = 17 2 = 289
Þ 2xy =240 Þ SABCD = 240cm2

Nối hai đường chéo của hình thoi lại=>Ta dc 4 tam giác bằng nhau trong hình thời đó.
Áp dụng định lí Pytago vào từng tam giác đó,ta tính đc:
Nửa mỗi đường chéo.
Từ đó ta tính dc các đg chéo của hình thoi.

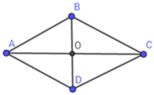
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, AB = 5 cm; BD = 6 cm.
Suy ra BO = 1 2 BD = 1 2 .6 = 3 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AO = A B 2 − O B 2 = 5 2 − 3 2 = 4
SABCD = 1 2 BD. AC = 1 2 BD. 2AO = BD.AO = 6.4 = 24 (cm2)
Đáp án cần chọn là: C

Nối 2 đường chéo của hình thoi lại => ta được 4 tam giác bằng nhau trong hình thời đó
Áp dụng định lý Pytago vào từng tam giác đó ta tính được :
Nửa mỗi đường chéo ta cũng tính được đường chéo hình thoi
Và tính diện tích hình thoi


diện tích hình thoi là :
\(\frac{1}{2}.\left(2.2\right).\left(2.2\right)=8\left(cm^2\right)\)
đáp số: ..........................
a: \(S_{\text{Δ}}=\dfrac{1}{2}\cdot6\cdot6\cdot sin60=9\sqrt{3}\left(cm^2\right)\)
=>Diện tích hình thoi là 9căn3*2=18căn 3(cm2)
b: S=30*40/2=30*20=600cm2