giúp mình vs mình đang vội
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
2
25 tháng 6 2021
19) Ta có: \(\sqrt[3]{x^3+9x^2}=x+3\)
\(\Leftrightarrow x^3+9x^2=\left(x+3\right)^3\)
\(\Leftrightarrow x^3+9x^2=x^3+9x^2+27x+27\)
\(\Leftrightarrow27x+27=0\)
\(\Leftrightarrow27x=-27\)
hay x=-1
Vậy: S={-1}
6) Ta có: \(\sqrt{9x^2-6x+1}-x=4\)
\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=x+4\)
\(\Leftrightarrow\left|3x-1\right|=x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+4\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+4\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-x=4+1\\-3x-x=4-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\-4x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(nhận\right)\\x=\dfrac{-3}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{5}{2};\dfrac{-3}{4}\right\}\)
25 tháng 6 2021
8)
ĐKXĐ: \(x>2\)
Ta có: \(\sqrt{x^2+2x+4}=x-2\)
\(\Leftrightarrow x^2+2x+4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2+2x+4-x^2+4x-4=0\)
\(\Leftrightarrow6x=0\)
hay x=0(loại)
Vậy: \(S=\varnothing\)
9) Ta có: \(\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\left|x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy: S={8;-2}
PN
1
NT
1
7 tháng 10 2021
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CM=CN
hay C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OC là đường trung trực của MN
PT
0
TT
1
TN
13 tháng 9 2018
7a có: \(\frac{1}{2}=x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)\(\Leftrightarrow x+y\le1\)
Áp dụng BD7 Cauchy-SChwarz 7a có:
\(V7=\frac{x}{y+1}+\frac{y}{x+1}=x-\frac{xy}{y+1}+y-\frac{xy}{x+1}\)
\(\le x+y-\frac{\left(x^2+y^2\right)}{2}\left(\frac{1}{y+1}+\frac{1}{x+1}\right)\)
\(\le1-\frac{\frac{1}{2}}{2}\cdot\frac{4}{1+2}=\frac{2}{3}=VP\)
Dấu "='' khi \(x=y=\frac{1}{4}\)
25 tháng 5 2021
`1)((sqrt{14}-sqrt7)/(1-sqrt2)+(sqrt{15}-sqrt5)/(1-sqrt3)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt2-1))/(1-sqrt2)+(sqrt5(sqrt3-1))/(1-sqrt3):1/(sqrt7-sqrt5)`
`=(-sqrt7-sqrt5):1/(sqrt7-sqrt5)`
`=-(sqrt7+sqrt5).(sqrt7-sqrt5)`
`=-(7-5)`
`=-2`
`2)B=(2sqrtx-9)/(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)-(2sqrtx+1)/(3-sqrtx)`
`=(2sqrtx-9-x+9+2x-3sqrtx-2)/(x-5sqrtx+6)`
`=(x-sqrtx-2)/(x-5sqrtx+6)`
`=((sqrtx-2)(sqrtx+1))/((sqrtx-2)(sqrtx-3))`
`=(sqrtx+1)/(sqrtx-3)`
`x=11+6sqrt2`
`=(3+sqrt2)^2`
`=>B=(4+2sqrt2)/(sqrt2)`
`=2+2sqrt2`
25 tháng 5 2021
`3)5x^4+4x^2-1=0`
Đặt `t=x^2(t>=0)`
`pt<=>5t^2+4t-1=0`
`a-b+c=0`
`=>t_1=-1(l),t_2=1/5(tm)`
`<=>x=+-sqrt{1/5}`
Vậy `S={-sqrt{1/5},+sqrt{1/5}}`
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
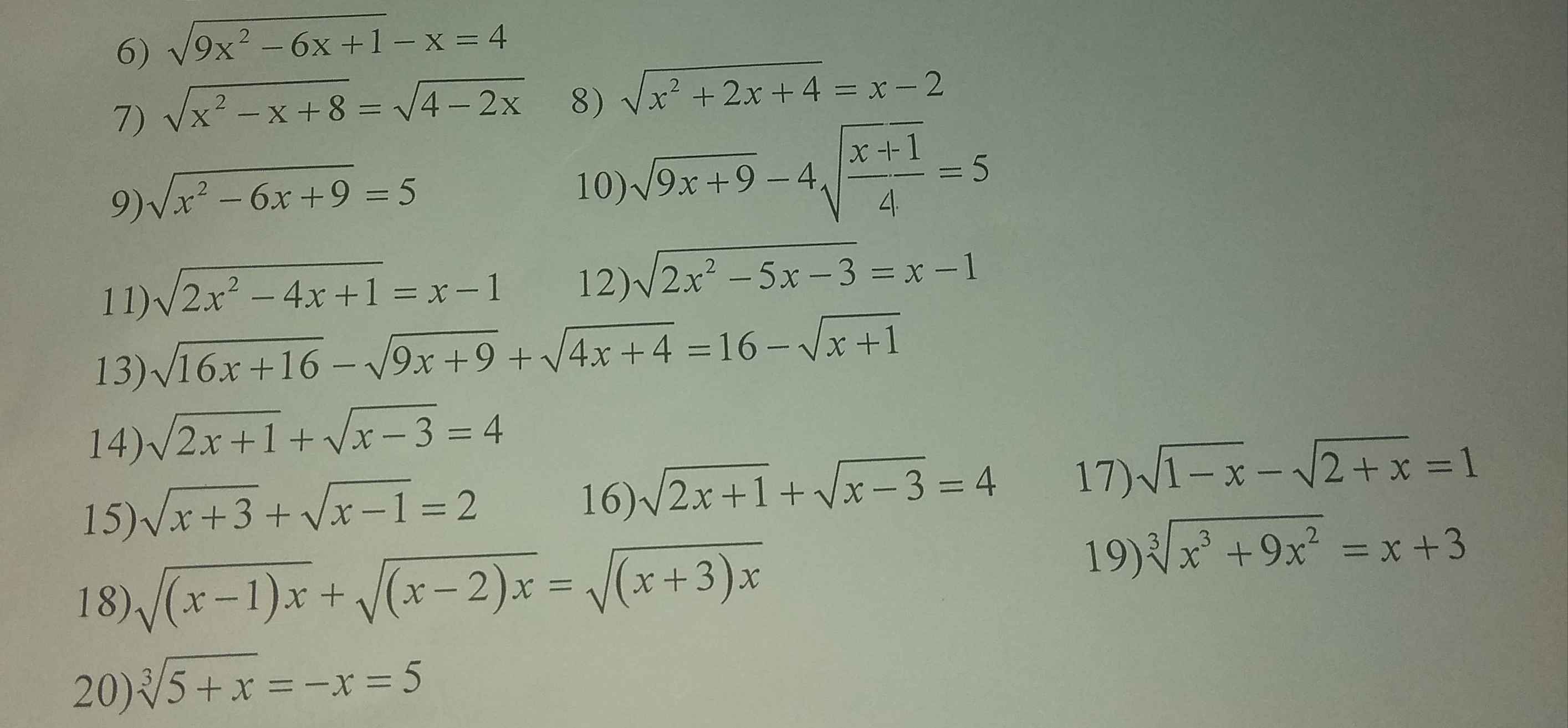
a) \(\sqrt{144}-\sqrt{9}-\sqrt{250}\cdot\sqrt{1,6}=12-3-20=-11\)
a) \(\frac{\sqrt{144}}{\sqrt{9}}-\sqrt{250}.\sqrt{1,6}\) = \(\frac{12}{3}-\sqrt{250.1,6}\) = \(4-\sqrt{25.16}\) = \(4-20=-16\)
b) \(\frac{\sqrt{3,6}}{\sqrt{4,9}}-\sqrt{3.2^3.24}\) = \(\sqrt{\frac{36}{49}}-\sqrt{576}\) = \(\frac{6}{7}-24=-\frac{162}{7}\)
c) \(\sqrt{2+\sqrt{3}}\) = \(\sqrt{3+2.\frac{\sqrt{3}}{2}+\frac{1}{4}-\frac{3}{4}}\) = \(\sqrt{\left(\sqrt{3}+\frac{1}{2}\right)^2-\left(\frac{\sqrt{3}}{2}\right)^2}\)
= \(\sqrt{\left(\sqrt{3}+\frac{1}{2}-\frac{\sqrt{3}}{2}\right)\left(\sqrt{3}+\frac{1}{2}+\frac{\sqrt{3}}{2}\right)}\)