K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
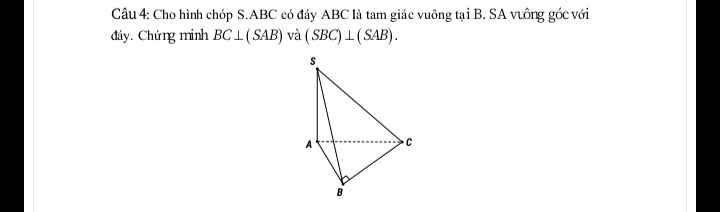
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Lại có \(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAB\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
Xét phương trình phần đường bao:
\(\left(x+3\right)^2+\left(y+1\right)^2=1\Leftrightarrow\left(y+1\right)^2=1-\left(x+3\right)^2\)
\(\Leftrightarrow y+1=\pm\sqrt{1-\left(x+3\right)^2}\) (với \(-4\le x\le-2\))
\(\Leftrightarrow y=-1\pm\sqrt{1-\left(x+3\right)^2}\)
\(V=\pi\int\limits^{-2}_{-4}\left[\left(-1-\sqrt{1-\left(x+3\right)^2}\right)^2-\left(-1+\sqrt{1-\left(x+3\right)^2}\right)^2\right]dx\)
\(=\pi\int\limits^{-2}_{-4}4\sqrt{1-\left(x+3\right)^2}dx\)
Đặt \(x+3=sint\Rightarrow dx=cost.dt\) ; \(\left\{{}\begin{matrix}x=-4\Rightarrow t=-\dfrac{\pi}{2}\\x=-2\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(V=\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}4cost.cost.dt=2\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left(1+cos2t\right)=\pi\left(t+\dfrac{1}{2}sin2t\right)|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}=2\pi^2\)
Có vẻ cả 4 đáp án đều không chính xác
8 tháng 10 2023
\(\left(x^2-1\right)'=2x;\left[\left(x-2\right)^4\right]'=4\cdot\left(x-2\right)^3\cdot\left(x-2\right)'=4\left(x-2\right)^3\)
\(f''\left(x\right)=\left(x^2-1\right)'\left(x-2\right)^4+\left(x^2-1\right)\left[\left(x-2\right)^4\right]'\)
\(=2x\left(x-2\right)^4+\left(x^2-1\right)\cdot4\left(x-2\right)^3\)
\(=2\left(x-2\right)^3\left[x\left(x-2\right)+2x^2-2\right]\)
\(=2\left(x-2\right)^3\left(3x^2-2x-2\right)\)
Đặt \(f'\left(x\right)=0\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\\x=2\end{matrix}\right.\)
\(f''\left(2\right)=0;f''\left(1\right)=2>0;f''\left(-1\right)=-162< 0\)
=>Chọn B
\(g'\left(x\right)=-f'\left(3-x\right)-\dfrac{2x}{3}\)
\(g'\left(x\right)=0\Rightarrow f'\left(3-x\right)=-\dfrac{2x}{3}=\dfrac{2}{3}\left(3-x\right)-2\)
Đặt \(3-x=t\Rightarrow f'\left(t\right)=\dfrac{2}{3}t-2\)
Từ đồ thị ta thấy \(y=\dfrac{2}{3}t-2\) cắt \(y=f'\left(t\right)\) tại 3 điểm: \(t=\left\{0;3;6\right\}\)
\(g'\left(x\right)\le0\Rightarrow f'\left(3-x\right)\ge\dfrac{2}{3}\left(3-x\right)-2\)
\(f'\left(t\right)\) nằm trên \(y=\dfrac{2}{3}t-2\) khi \(\left[{}\begin{matrix}t< 0\\3< t< 6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3-x< 0\\3< 3-x< 6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>3\\-3< x< 0\end{matrix}\right.\)
A đúng