
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay x=2 và y=3 vào (d), ta đc:
m-1+2=3
=>m+1=3
=>m=2
b: Vì (d)//y=2x+1 nên a=2
=>(d): y=2x+b
THay y=2 vào y=3x+5, ta đc:
3x+5=2
=>3x=-3
=>x=-1
Thay x=-1 và y=2 vào y=2x+b, ta được:
b-2=2
=>b=4

Bài 1:
\(\sqrt{9-4\sqrt{2}}-3\sqrt{16-6\sqrt{7}}=\sqrt{8+1-2\sqrt{8.1}}-3\sqrt{9+7-2\sqrt{9.7}}\)
\(=\sqrt{(\sqrt{8}-1)^2}-3\sqrt{(\sqrt{9}-\sqrt{7})^2}\)
\(=\sqrt{8}-1-3(\sqrt{9}-\sqrt{7})=-10+2\sqrt{2}+3\sqrt{7}\)

1: Thay x=16 vào A, ta được:
\(A=\dfrac{16-4}{4-2}=\dfrac{12}{2}=6\)
2: \(B=\dfrac{x-4+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{x-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)


bạn đăng ít thôi cho mn cùng giúp nhé
a, \(x^2-2\sqrt{5}x+5=0\Leftrightarrow\left(x-\sqrt{5}\right)^2=0\Leftrightarrow x=\sqrt{5}\)
b, \(x^2-9x+10=0\)
\(\Delta=81-4.10=41>0\)
\(x_1=\dfrac{9-\sqrt{41}}{2};x_2=\dfrac{9+\sqrt{41}}{2}\)
c, \(2x^2-3x+5=0\)
\(\Delta=9-4.5.2=9-40< 0\)
Vậy pt vô nghiệm

Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)

Cho mình hỏi : A = ( x thuộc N / 2x + 2 ; x bé hơn 100 mình cần gấp lắm rồi,
8:
a: Để đây là hsbn thì m-1<>0
=>m<>1
b: Để hàm số đồng biến thì m-1>0
=>m>1
Để hàm số nghịch biến thì m-1<0
=>m<1
c: Thay x=3 và y=4 vào (d) ta được:
3(m-1)+5=4
=>3m+2=4
=>3m=2
=>m=2/3

Bài 4:
ĐKXĐ: \(x\ge3\)
Ta có: \(\sqrt{x^2-9}-\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)


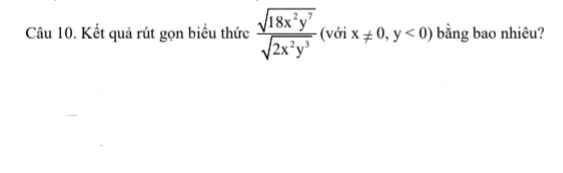
 . Giúp mình với nhé cảm ơn nhiều!
. Giúp mình với nhé cảm ơn nhiều!
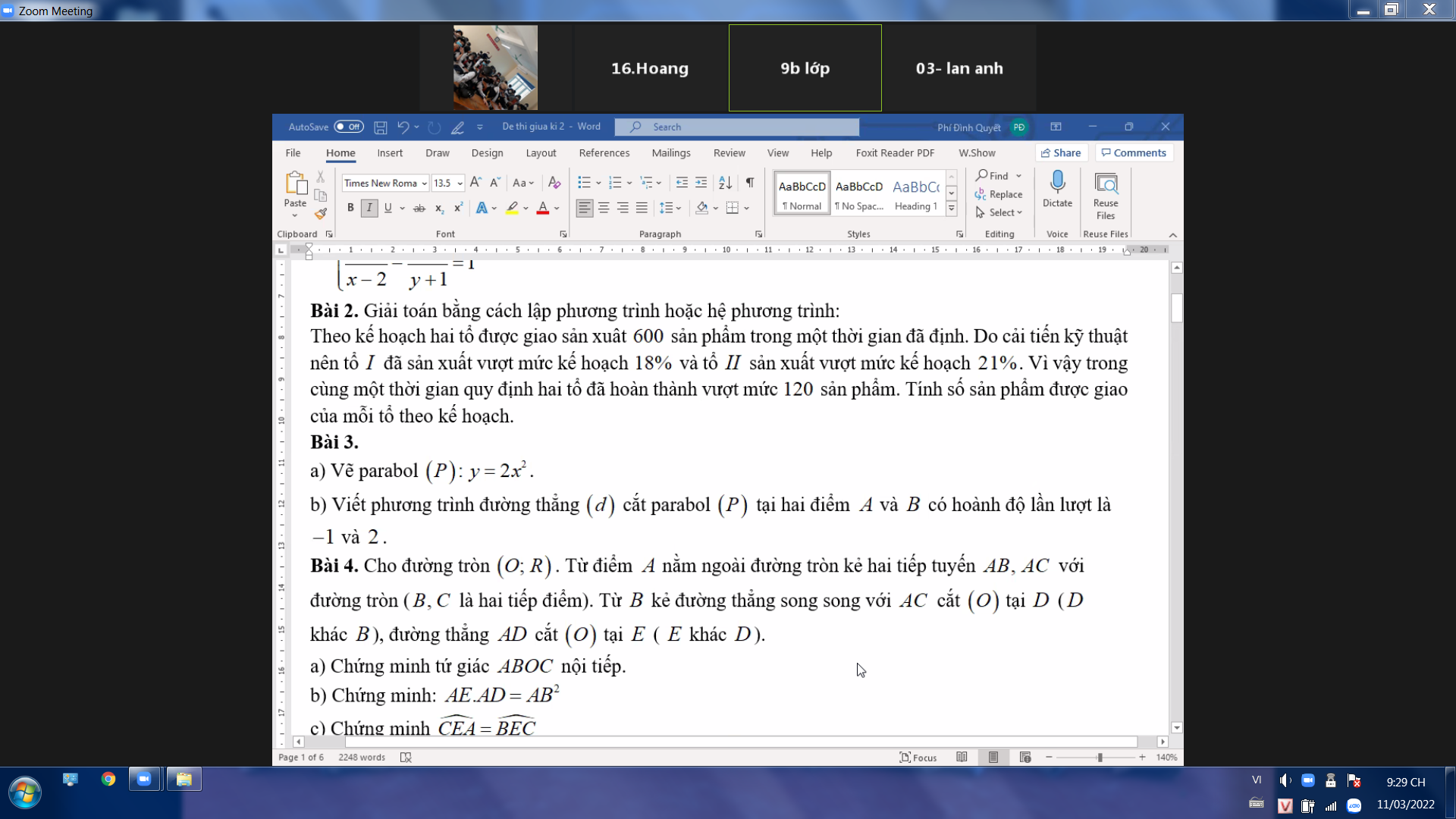
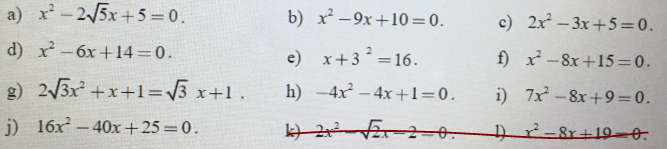 GIÚP MÌNH CÂU KHÔNG GẠCH ĐỎ VỚI NHÉ!
GIÚP MÌNH CÂU KHÔNG GẠCH ĐỎ VỚI NHÉ!

\(a,VT=\left(\sin^252^0+\sin^238^0\right)-\left(\tan37^0-\cot53^0\right)+\dfrac{\tan42^0}{\tan42^0}\\ =\left(\sin^252^0+\cos^252^0\right)-\left(\tan37^0-\tan37^0\right)+1\\ =1-0+1=2=VP\\ c,VT=\dfrac{2\cos^2\alpha-\sin^2\alpha-\cos^2\alpha}{\sin\alpha+\cos\alpha}=\dfrac{\cos^2\alpha-\sin^2\alpha}{\sin\alpha+\cos\alpha}\\ =\dfrac{\left(\cos\alpha-\sin\alpha\right)\left(\cos\alpha+\sin\alpha\right)}{\cos\alpha+\sin\alpha}=\cos\alpha-\sin\alpha=VP\\ b,VT=\cos^2\alpha+\cos^2\alpha\cdot\dfrac{\sin^2\alpha}{\cos^2\alpha}=\cos^2\alpha+\sin^2\alpha=1=VP\)