
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


13) để căn thức xác định \(\Rightarrow\dfrac{2x-4}{-2}\ge0\) mà \(-2< 0\Rightarrow2x-4\le0\)
\(\Rightarrow x-2\le0\Rightarrow x\le2\)
14) để căn thức xác định \(\Rightarrow-\dfrac{2}{x-2}\ge0\Rightarrow\dfrac{2}{x-2}\le0\)
mà \(2>0\Rightarrow x-2< 0\Rightarrow x< 2\)
15) để căn thức xác định \(\Rightarrow\dfrac{2\sqrt{15}-\sqrt{59}}{7-x}\ge0\)
Ta có: \(2\sqrt{15}=\sqrt{60}>\sqrt{59}\left(60>59\right)\Rightarrow2\sqrt{15}-\sqrt{59}>0\)
\(\Rightarrow7-x>0\Rightarrow x< 7\)
3) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}1-x\ge0\\3-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le1\\x\le3\end{matrix}\right.\Rightarrow x\le1\)
4) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}15-3x\ge0\\5-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le5\\x\le5\end{matrix}\right.\Rightarrow x\le5\)
5) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}3x-9\ge0\\9-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge3\\x\le9\end{matrix}\right.\Rightarrow3\le x\le9\)
Bài 1:
1) \(\sqrt{2}< \sqrt{3}\)
2) \(\sqrt{3}< \sqrt{10}\)
3) \(2\sqrt{3}>2\sqrt{2}\)
4) \(3\sqrt{3}< 3\sqrt{5}\)
5) \(5\sqrt{2}>3\sqrt{2}\)
6) \(-5\sqrt{3}< -3\sqrt{3}\)


9:
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-2m+4\right)\)
=4m^2-4m^2+8m-16=8m-16
Để phương trình có hai nghiệm phân biệt thì 8m-16>0
=>m>2
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+4)-2m=8
=>4m^2-2m^2+4m-8-2m=8
=>2m^2+2m-16=0
=>m^2+m-8=0
mà m>2
nên \(m=\dfrac{-1+\sqrt{33}}{2}\)


\(Q=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\dfrac{2}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}-1=Ư\left(2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=-2\\\sqrt{x}-1=-1\\\sqrt{x}-1=1\\\sqrt{x}-1=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=-1\left(vn\right)\\\sqrt{x}=0\\\sqrt{x}=2\\\sqrt{x}=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=9\end{matrix}\right.\)

\(a,=\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)\\ b,=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-2\left(\sqrt{x}+\sqrt{y}\right)\\ =\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}-2\right)\\ c,=x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)\)
\(a,=\dfrac{\left(9-4\sqrt{5}\right)\left(5+2\sqrt{5}\right)}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{5-2\sqrt{5}}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{25-10\sqrt{5}+8\sqrt{5}}{20}=\dfrac{25-2\sqrt{5}}{20}\\ b,=\dfrac{\sqrt{x}+2-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\\ c,=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}-\dfrac{2}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}+1-2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}=1\\ d,=\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}+\dfrac{x+1}{1-x}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)

Câu V:
a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot DB\)
=>\(\dfrac{AB^2}{AD^2}=\dfrac{BH\cdot BD}{DH\cdot DB}=\dfrac{BH}{DH}\)
=>\(\dfrac{BH}{DH}=\dfrac{CD^2}{BC^2}=\left(\dfrac{CD}{BC}\right)^2=\left(\dfrac{CD}{3CD}\right)^2=\dfrac{1}{9}\)
=>\(DH=9BH\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
=>\(9\cdot BH\cdot BH=\left(3\sqrt{10}\right)^2=90\)
=>\(BH^2=10\)
=>\(BH=\sqrt{10}\left(cm\right)\)
=>\(DH=9\sqrt{10}\left(cm\right)\)
\(BD=BH+DH=10\sqrt{10}\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot BD\)
=>\(AB^2=\sqrt{10}\cdot10\sqrt{10}=100;AD^2=9\sqrt{10}\cdot\sqrt{10}=90\)
=>\(AB=10\left(cm\right);AD=3\sqrt{10}\left(cm\right)\)
Chu vi hình chữ nhật ABCD là:
\(C_{ABCD}=\left(AB+AD\right)\cdot2=\left(10+3\sqrt{2}\right)\cdot2\left(cm\right)\)
b: Xét ΔHAD có
M,I lần lượt là trung điểm của HD,HA
=>MI là đường trung bình của ΔHAD
=>MI//AD
Ta có: MI//AD
AB\(\perp\)AD
Do đó: MI\(\perp\)AB
Xét ΔMAB có
MI,AH là các đường cao
MI cắt AH tại I
Do đó: I là trực tâm của ΔMAB
=>BI\(\perp\)AM

Em chụp ảnh rõ hơn, mỗi câu hỏi chỉ đăng 1 bài, và chỉ đăng nhờ trợ giúp bài chưa làm được thui nha!
1.31:
a: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2
=>AD*AB=AE*AC
b: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC và AC^2=CH*BC
=>AB^2/AC^2=(BH*BC)/(CH*BC)=BH/CH
c: BD/CE
=BH^2/AB:CH^2/AC
\(=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}=\left(\dfrac{BH}{CH}\right)^2\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)
d: BC*BD*CE
\(=BC\cdot\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{AC}\)
\(=\dfrac{BC}{BA\cdot AC}\cdot AH^4=\dfrac{AH^4}{AH}=AH^3\)
e: Đặt HB=x; HC=y(x<y)
AH^2=HB*HC
=>x*y=16
HB+HC=BC
=>x+y=10
xy=16 và x+y=10
=>x,y là các nghiệm của phương trình:
a^2-10a+16=0
=>a=2 hoặc a=8
mà x<y
nên x=2 và y=8
=>BH=2cm; CH=8cm



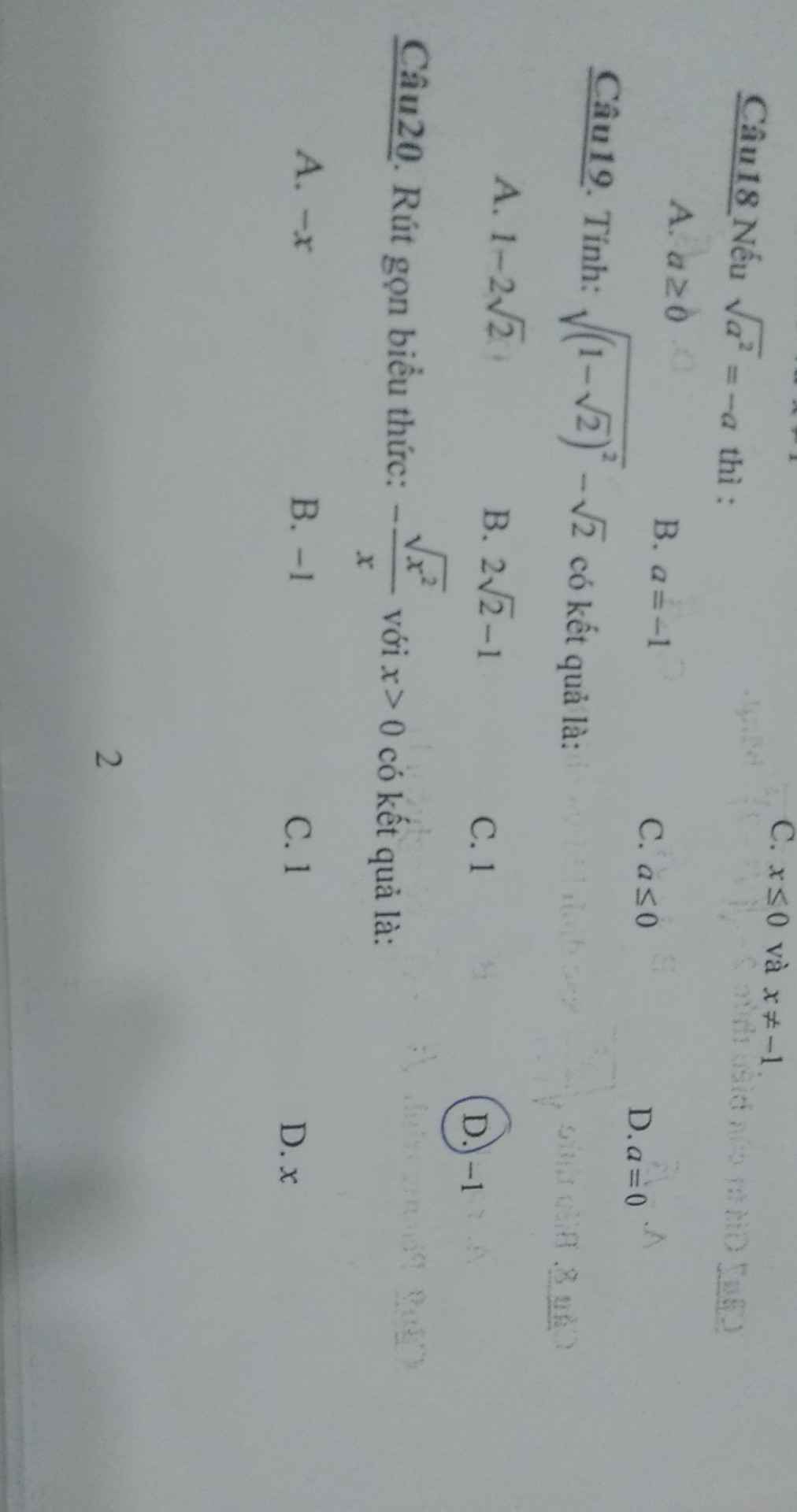
 Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai
Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai







ta có :