
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\sqrt{x}-\sqrt{x}+2}{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=-\sqrt{x}\cdot\left(\sqrt{x}+1\right)\)


Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)

Câu 2
a, Thay \(m=-2\) vào \(\left(1\right)\)
\(x^2-2x+\left(-2\right)-1=0\\ \Rightarrow x^2-2x-3=0\\ \Delta=\left(-2\right)^2-4.1.\left(-3\right)=16\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2+4}{2}=3\\x_2=\dfrac{2-4}{2}=-1\end{matrix}\right.\)
Vậy với m =-1 thì phương trình có hai nghiệm x =3 ; x= -1
2, \(\Delta=\left(-2\right)^2-4.1.\left(m-1\right)=4-4m+4\\ =-4m+8\)
phương trình có hai nghiệm phân biệt \(\Delta>0\\ \Rightarrow-4m+8>0\\ \Leftrightarrow m< 2\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{matrix}\right.\)
Kết hợp \(\left(1\right)\) và \(x_1+2x_2=0\) ta có hệ
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1+2x_2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-2\end{matrix}\right.\)
Thay \(x_1=4;x_2=-2\) vào 2
\(\Rightarrow4.\left(-2\right)=m-1\\ \Rightarrow m=-7\left(t/m\right)\)
Vậy \(m=-7\)
Câu 1:
\(\left\{{}\begin{matrix}2x+y=5\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{5}=2\\3.2-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\6-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)

Giải hpt:
Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)
Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

6.
\(0,3a^3b^2\sqrt{\dfrac{9}{a^4b^8}}=0,3a^3b^2.\dfrac{3}{a^2b^4}=\dfrac{0,9.a}{b^2}\)
Đáp án B
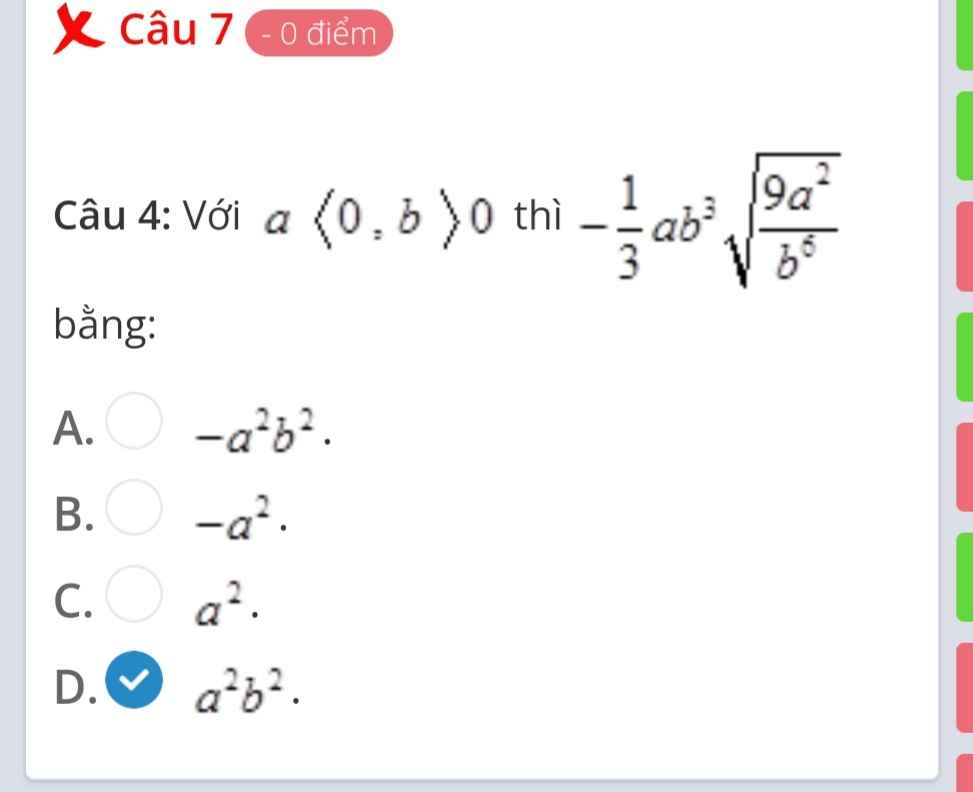
7.
\(-\dfrac{1}{3}ab^3\sqrt{\dfrac{9a^2}{b^6}}=-\dfrac{1}{3}ab^3.\dfrac{3\left|a\right|}{\left|b^3\right|}=-ab^3.\dfrac{-a}{b^3}=a^2\)
Đáp án C



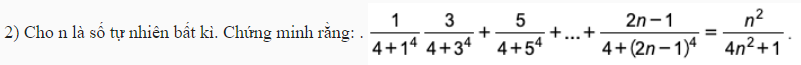
 Giúp em câu 2 với ạ. Em cảm ơn nhiều
Giúp em câu 2 với ạ. Em cảm ơn nhiều



Câu V:
a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot DB\)
=>\(\dfrac{AB^2}{AD^2}=\dfrac{BH\cdot BD}{DH\cdot DB}=\dfrac{BH}{DH}\)
=>\(\dfrac{BH}{DH}=\dfrac{CD^2}{BC^2}=\left(\dfrac{CD}{BC}\right)^2=\left(\dfrac{CD}{3CD}\right)^2=\dfrac{1}{9}\)
=>\(DH=9BH\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
=>\(9\cdot BH\cdot BH=\left(3\sqrt{10}\right)^2=90\)
=>\(BH^2=10\)
=>\(BH=\sqrt{10}\left(cm\right)\)
=>\(DH=9\sqrt{10}\left(cm\right)\)
\(BD=BH+DH=10\sqrt{10}\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot BD\)
=>\(AB^2=\sqrt{10}\cdot10\sqrt{10}=100;AD^2=9\sqrt{10}\cdot\sqrt{10}=90\)
=>\(AB=10\left(cm\right);AD=3\sqrt{10}\left(cm\right)\)
Chu vi hình chữ nhật ABCD là:
\(C_{ABCD}=\left(AB+AD\right)\cdot2=\left(10+3\sqrt{2}\right)\cdot2\left(cm\right)\)
b: Xét ΔHAD có
M,I lần lượt là trung điểm của HD,HA
=>MI là đường trung bình của ΔHAD
=>MI//AD
Ta có: MI//AD
AB\(\perp\)AD
Do đó: MI\(\perp\)AB
Xét ΔMAB có
MI,AH là các đường cao
MI cắt AH tại I
Do đó: I là trực tâm của ΔMAB
=>BI\(\perp\)AM