K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2021
a) \(x^2-6x+10=\left(x^2-6x+9\right)+1\)
\(=\left(x-3\right)^2+1\ge1>0\forall x\)
b) \(4x-x^2-5=-\left(x^2-4x+4\right)-1\)
\(=-\left(x-2\right)^2-1\le-1< 0\forall x\)
1 tháng 11 2021
\(a,A=\left(5x-1+1-x\right)^2=16x^2\\ B=x^3-x^3+4x=4x\\ c,A=B\Leftrightarrow16x^2-4x=0\\ \Leftrightarrow4x\left(4x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\)
9 tháng 11 2021
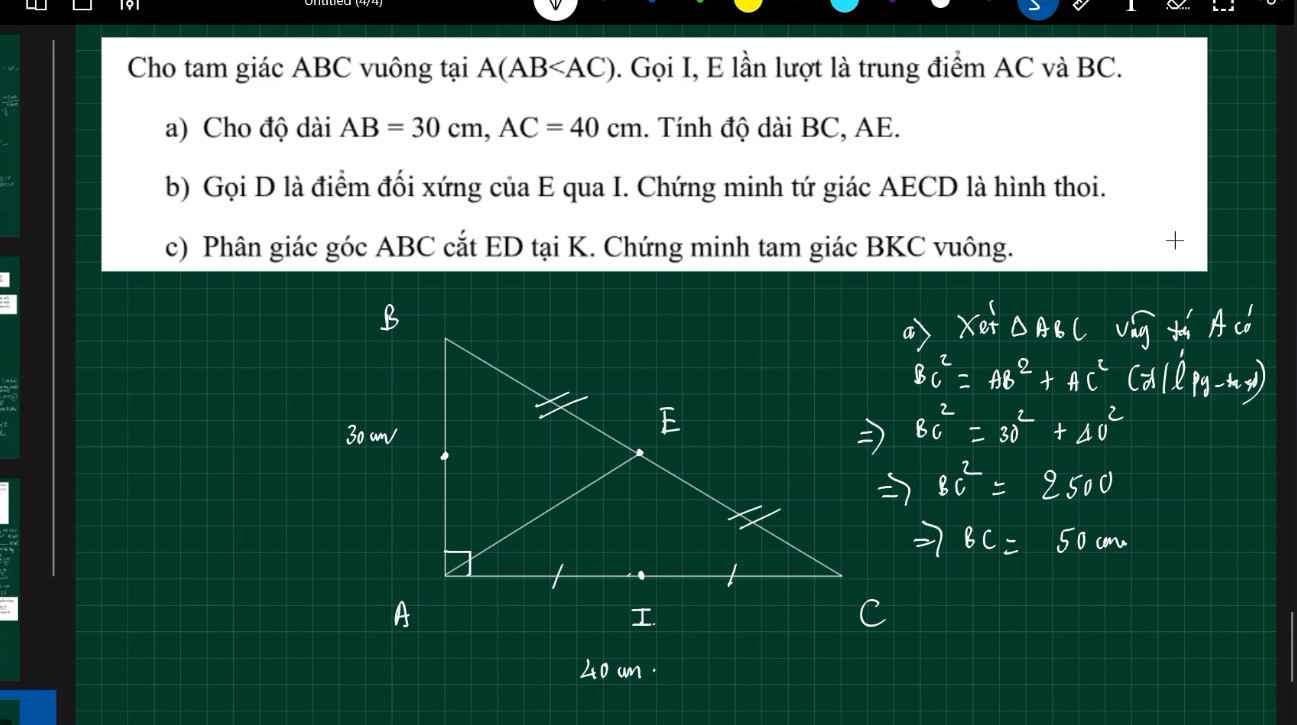
a: Xét ΔABC có
N là trung điểm của AC
M là trung điểm của BC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//AB
hay ABMN là hình thang
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 6 2023
A = \(x^2\) - 4\(x\) + 2018
A = \(x^2\) - 4\(x\) + 4 + 2014
A= (\(x\) - 2)2 + 2014
Vì (\(x\) - 2)2 ≥ 0; ⇒ (\(x\) - 2)2 + 2014 ≥ 2014
A(min) = 2014 ⇔ \(x\) - 2= 0 ⇔ \(x\) = 2
Kết luận giá trị nhỏ nhất của biểu thức A là 2014 xảy ra khi \(x\) = 2
B = 4\(x^2\) + 12\(x\) + 20
B = (4\(x^2\) + 12\(x\) + 9) + 11
B = 4.(\(x^2\) + 3\(x\) + \(\dfrac{9}{4}\)) + 11
B =4.(\(x^2\) + 2.\(\dfrac{3}{2}\)\(x\) + \(\left(\dfrac{3}{2}\right)^2\)) + 11
B = 4.(\(x\) + \(\dfrac{3}{2}\))2 + 11
Vì (\(x\) + \(\dfrac{3}{2}\))2 ≥ 0 ⇒ 4.(\(x\) + \(\dfrac{3}{2}\))2 + 11 ≥ 11
Vậy B(min) = 11 ⇔ \(x\) + \(\dfrac{3}{2}\) = 0⇔ \(x\) = - \(\dfrac{3}{2}\)
Kết luận giá trị nhỏ nhất của biểu thức B là: 11 xảy ra khi \(x\) = - \(\dfrac{3}{2}\)
4 tháng 6 2023
A = - 4 + 2018
A = - 4 + 4 + 2014
A= ( - 2)2 + 2014
Vì ( - 2)2 ≥ 0; ⇒ ( - 2)2 + 2014 ≥ 2014
A(min) = 2014 ⇔ - 2= 0 ⇔ = 2
Kết luận giá trị nhỏ nhất của biểu thức A là 2014 xảy ra khi = 2
B = 4 + 12 + 20
B = (4 + 12 + 9) + 11
B = 4.( + 3 + ) + 11
B =4.( + 2. + ) + 11
B = 4.( + )2 + 11
Vì ( + )2 ≥ 0 ⇒ 4.( + )2 + 11 ≥ 11
Vậy B(min) = 11 ⇔ + = 0⇔ = -
Kết luận giá trị nhỏ nhất của biểu thức B là: 11 xảy ra khi = -
VT
1