
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) \(=\dfrac{\sqrt{5}.\sqrt{7}}{5}=\dfrac{\sqrt{35}}{5}\)
b) \(=\dfrac{\left|y\right|}{\sqrt{3}}=\dfrac{\sqrt{3}y}{3}\)
c) \(=\dfrac{\sqrt{2}}{\sqrt{t}}=\dfrac{\sqrt{2t}}{t}\)
d) \(=\sqrt{\dfrac{7p^2-3p^2}{7}}=\sqrt{\dfrac{4p^2}{7}}=\dfrac{2\left|p\right|}{\sqrt{7}}=\dfrac{-2\sqrt{7}p}{7}\)
Bài 2:
a) \(=\dfrac{\sqrt{21}-\sqrt{15}}{3}\)
b) \(=\dfrac{10\left(4+3\sqrt{2}\right)}{16-18}=-20-15\sqrt{2}\)
c) \(=\dfrac{\left(3\sqrt{10}-5\right)\left(6+\sqrt{10}\right)}{36-10}=\dfrac{18\sqrt{10}+30-30-5\sqrt{10}}{26}=\dfrac{13\sqrt{10}}{26}=\dfrac{\sqrt{10}}{2}\)

b: \(BC\cdot\sin B\cdot\sin C\)
\(=BC\cdot\dfrac{AC}{BC}\cdot\dfrac{AB}{BC}\)
\(=\dfrac{BC\cdot AH\cdot BC}{BC^2}=AH\)

d: Để (d1) vuông góc với y=(k-1)x+4 thì \(\left(k-1\right)\left(k-3\right)=-1\)
\(\Leftrightarrow k=2\)

B3
1) \(\sqrt{ }\)(2x-1)2 =5
\(\Leftrightarrow\) |2x-1| =5
\(\Leftrightarrow\) 2x-1 =5 hoặc 2x -1 = -5
\(\Leftrightarrow\) 2x=6 hoặc 2x= -4
\(\Leftrightarrow\) x=3 hoặc x= -2
2) 4-5x = 144
\(\Leftrightarrow\) -5x =140
\(\Leftrightarrow\) x= -60
3) \(\sqrt{ }\)(2x-2)2=2x-2
\(\Leftrightarrow\) | 2x -2 | =2x-2
\(\Leftrightarrow\) 2x-2 =2x-2 hoặc 2x-2 =-2x +2
\(\Leftrightarrow\) 0x=0 (loại ) hoặc x=2 ( nhận )

19) Ta có: \(\sqrt[3]{x^3+9x^2}=x+3\)
\(\Leftrightarrow x^3+9x^2=\left(x+3\right)^3\)
\(\Leftrightarrow x^3+9x^2=x^3+9x^2+27x+27\)
\(\Leftrightarrow27x+27=0\)
\(\Leftrightarrow27x=-27\)
hay x=-1
Vậy: S={-1}
6) Ta có: \(\sqrt{9x^2-6x+1}-x=4\)
\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=x+4\)
\(\Leftrightarrow\left|3x-1\right|=x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+4\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+4\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-x=4+1\\-3x-x=4-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\-4x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(nhận\right)\\x=\dfrac{-3}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{5}{2};\dfrac{-3}{4}\right\}\)
8)
ĐKXĐ: \(x>2\)
Ta có: \(\sqrt{x^2+2x+4}=x-2\)
\(\Leftrightarrow x^2+2x+4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2+2x+4-x^2+4x-4=0\)
\(\Leftrightarrow6x=0\)
hay x=0(loại)
Vậy: \(S=\varnothing\)
9) Ta có: \(\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\left|x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy: S={8;-2}

Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)

10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1

ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.
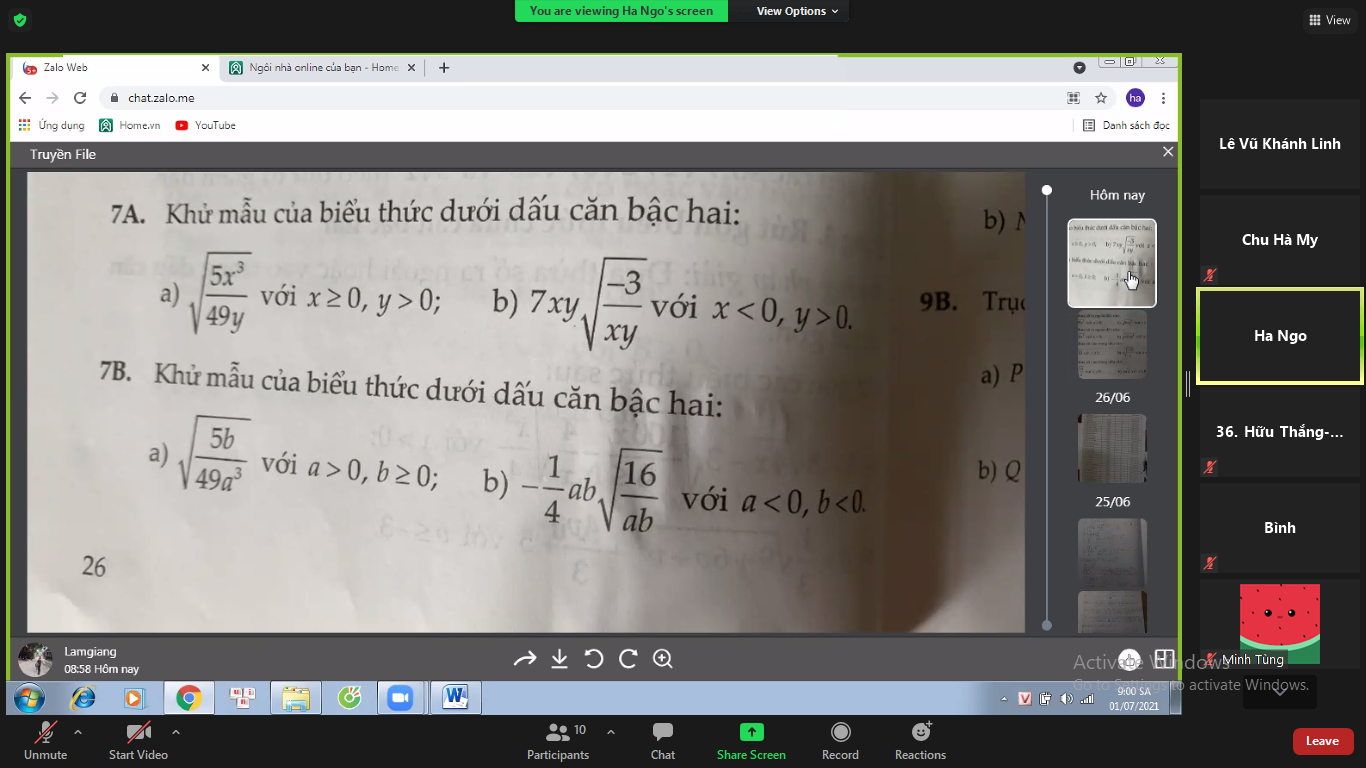







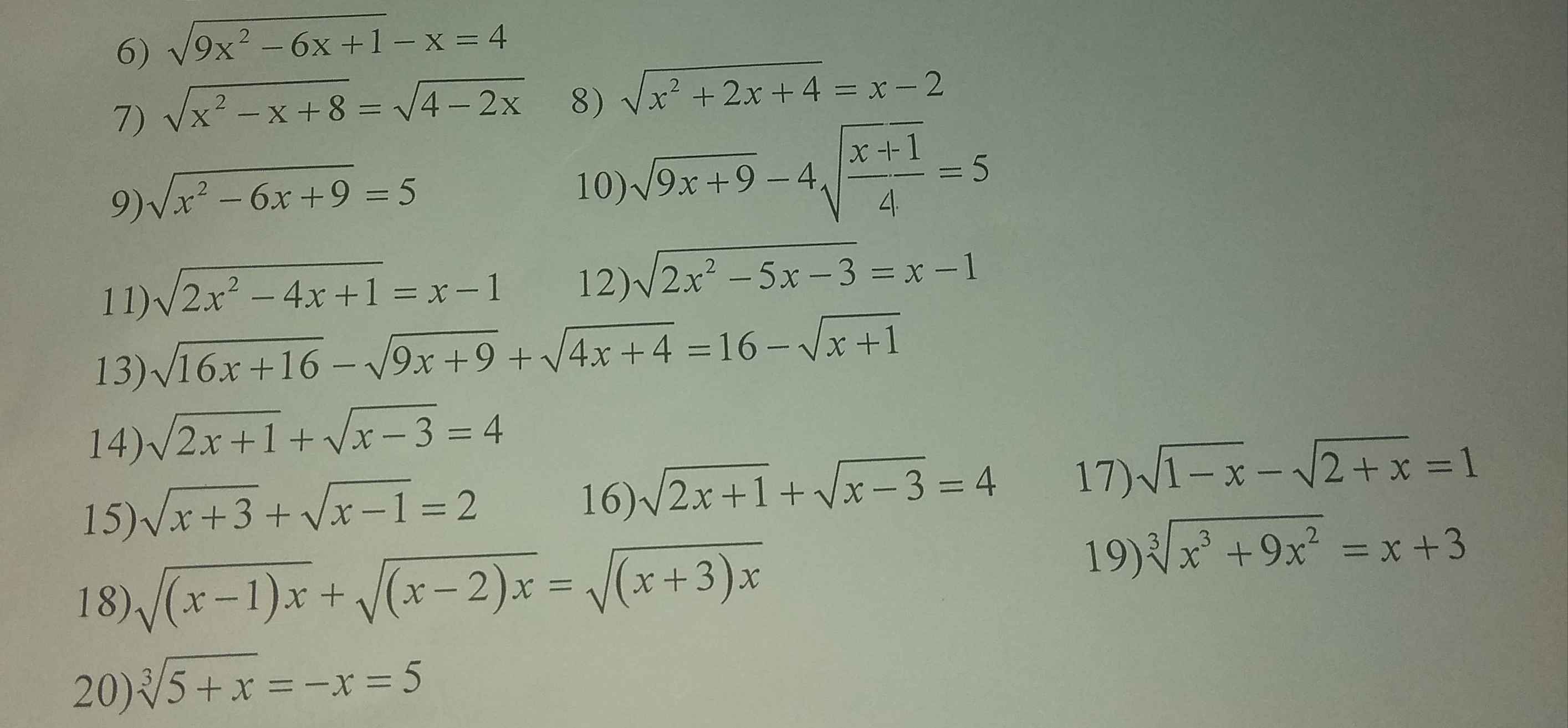




7A:
a) \(\sqrt{\dfrac{5x^3}{49y}}=\dfrac{\sqrt{5x^3}}{7\sqrt{y}}=\dfrac{\sqrt{5x^3y}}{7y}\)
b) \(7xy\sqrt{-\dfrac{3}{xy}}=7xy\cdot\dfrac{\sqrt{-3xy}}{xy}=7\sqrt{-3xy}\)
7B:
a) \(\sqrt{\dfrac{5b}{49a^3}}=\dfrac{\sqrt{5b}}{7a\sqrt{a}}=\dfrac{\sqrt{5ab}}{7a^2}\)
b) \(-\dfrac{1}{4}ab\sqrt{\dfrac{16}{ab}}=-\dfrac{1}{4}\cdot ab\cdot\dfrac{4\sqrt{ab}}{ab}=-\sqrt{ab}\)