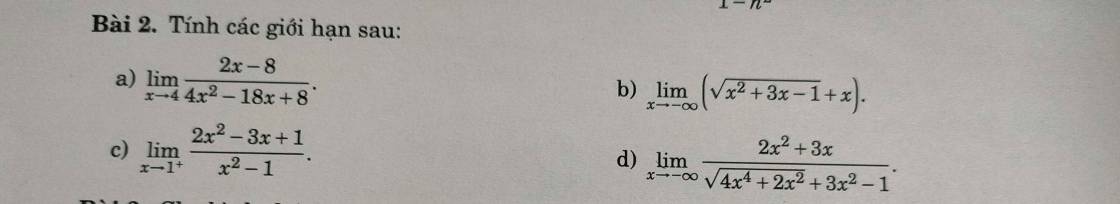Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(IM=\dfrac{1}{4}IB\Rightarrow IM=\dfrac{1}{5}BM\Rightarrow\overrightarrow{MI}=\dfrac{1}{5}\overrightarrow{MB}=-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(\Rightarrow\overrightarrow{DI}=\overrightarrow{DM}+\overrightarrow{MI}=\dfrac{1}{2}\overrightarrow{DC}-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)=\dfrac{1}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{DI}=\dfrac{2}{5}\overrightarrow{BC}-\dfrac{3}{5}\overrightarrow{BD}\)
\(\overrightarrow{DJ}=\overrightarrow{DC}+\overrightarrow{CJ}=\overrightarrow{DB}+\overrightarrow{BC}+x.\overrightarrow{CB}=\left(1-x\right)\overrightarrow{BC}-\overrightarrow{BD}\)
D; I; J thẳng hàng \(\Rightarrow\dfrac{1-x}{\dfrac{2}{5}}=\dfrac{1}{\dfrac{3}{5}}\Rightarrow x=\dfrac{1}{3}\)
\(\Rightarrow CJ=\dfrac{1}{3}CB\Rightarrow BJ=\dfrac{2}{3}BC\Rightarrow\dfrac{BJ}{BC}=\dfrac{2}{3}\)
Gọi N là trung điểm AD \(\Rightarrow\dfrac{BG}{BN}=\dfrac{2}{3}\) (theo t/c trọng tâm)
\(\Rightarrow\dfrac{BJ}{BC}=\dfrac{BG}{BN}\Rightarrow JG||CN\)
\(\Rightarrow\widehat{\left(JG;CD\right)}=\widehat{\left(CN;CD\right)}=\widehat{NCD}=30^0\) (do tam giác ACD đều)

2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)

c: \(\left(x^2+x-3\right)'=2x+1\)
(2x-1)'=2
\(y'=\dfrac{\left(2x+1\right)\cdot\left(2x-1\right)-\left(x^2+x-3\right)\cdot2}{\left(2x-1\right)^2}\)
\(=\dfrac{4x^2-1-2x^2-2x+6}{\left(2x-1\right)^2}=\dfrac{2x^2-2x+5}{\left(2x-1\right)^2}\)

\(\orbr{\begin{cases}2x+\frac{\pi}{6}=x+k2\pi\\2x+\frac{\pi}{6}=\pi-x+k2\pi\end{cases}}\) \(\Rightarrow\orbr{\begin{cases}x=-\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{18}+\frac{k2\pi}{3}\end{cases}}\)

a.
\(y'=4x^3-8x\)
b.
\(y'=\dfrac{2\left(5x+1\right)-5\left(2x-3\right)}{\left(5x+1\right)^2}=\dfrac{17}{\left(5x+1\right)^2}\)
c.
\(y'=\dfrac{\left(2x+1\right)\left(2x-1\right)-2\left(x^2+x-3\right)}{\left(2x-1\right)^2}=\dfrac{2x^2-2x+5}{\left(2x-1\right)^2}\)
d.
\(y'=\dfrac{\left(x^2-2x\right)'}{2\sqrt{x^2-2x+5}}=\dfrac{x-1}{\sqrt{x^2-2x+5}}\)

\(\lim\limits_{x\rightarrow4}\dfrac{2x-8}{4x^2-18x+8}=\lim\limits_{x\rightarrow4}\dfrac{2\left(x-4\right)}{2\left(x-4\right)\left(2x-1\right)}=\lim\limits_{x\rightarrow4}\dfrac{1}{2x-1}=-\dfrac{1}{7}\)
b.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+3x-1}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(\sqrt{x^2+3x-1}+x\right)\left(\sqrt{x^2+3x-1}-x\right)}{\sqrt{x^2+3x-1}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{3x-1}{\sqrt{x^2+3x-1}-x}=\lim\limits_{x\rightarrow-\infty}\dfrac{3-\dfrac{1}{x}}{-\sqrt{1+\dfrac{3}{x}-\dfrac{1}{x^2}}-1}=\dfrac{3-0}{-\sqrt{1+0-0}-1}=-\dfrac{3}{2}\)
c.
\(\lim\limits_{x\rightarrow1^+}\dfrac{2x^2-3x+1}{x^2-1}=\lim\limits_{x\rightarrow1^+}\dfrac{\left(x-1\right)\left(2x-1\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1^+}\dfrac{2x-1}{x+1}=\dfrac{1}{2}\)
d.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2+3x}{\sqrt{4x^4+2x^2}+3x^2-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(2+\dfrac{3}{x}\right)}{x^2\left(\sqrt{4+\dfrac{2}{x^2}}+3-\dfrac{1}{x^2}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{2+\dfrac{3}{x}}{\sqrt{4+\dfrac{2}{x^2}}+3-\dfrac{1}{x^2}}=\dfrac{2+0}{\sqrt{4+0}+3-0}=\dfrac{2}{5}\)

ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)
Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)
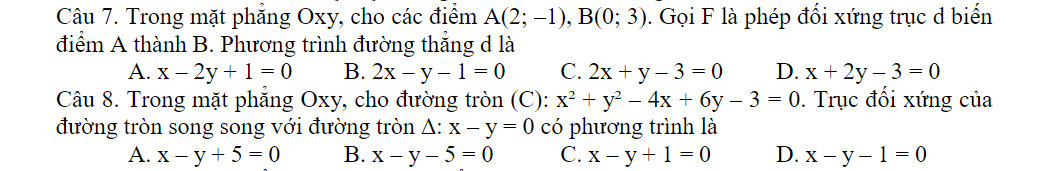 Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều