NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
0
13 tháng 5 2023
Cái này bạn nhận xét thôi: số cách xếp sao cho ko có bạn nào cùng lớp bằng số cách xếp sao cho ba bạn M2,N2,P2(Với M2,N2,P2 là 3 bạn của lớp A1) ko đứng cạnh nhau trừ đi số cách xếp sao cho ba bạn M2,N2,P2 ko đứng cạnh nhau và hai bạn M1,N1(M1,N1 là hai bạn của lớp A1) đứng cạnh nhau
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Do \(0\le cos^2x\le1\Rightarrow\dfrac{1}{2}\le y\le2\)
\(y_{min}=\dfrac{1}{2}\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
\(y_{max}=2\) khi \(cos^2x=1\Rightarrow sinx=0\Rightarrow x=k\pi\)
)
25 tháng 1 2023
👍🏻 Cách 1.
Như trên hình là số thứ tự các ghế
❤️ Trường hợp 1
Ghế có số lẻ là ghế các bạn nữ thì
G1 có 4 lựa chọn
G3 có 3 lựa chọn
G5 có 2 lựa chọn
G1 có 1 lựa chọn
Các ghế chẵn là nam
G2 có 4 lựa chọn
G4 có 3 lựa chọn
G6 có 2 lựa chọn
G8 có 1 lựa chọn
==> Với trường hợp 1 sẽ có
(4x3x2x1)x(4x3x2x1)=576 cách xếp
❤️ Trường hợp 2
Các ghế lẻ là nam và các ghế chẵn là nữ thì tương tự ta cũng có 576 cách xếp
=> Với cách 1 ta có
2x576=1152 cách xếp
25 tháng 1 2023
Cách 2 xếp 2 bàn ngược lại với cách 1 thì ta cũng sẽ có
1152 cách xếp
=> Với 2 cách xếp + 4 trường hợp ta có
2x1152=2304 cách xếp
HP
15 tháng 9 2021
1.
\(sin\left(x-\dfrac{\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow y=2sin\left(x-\dfrac{\pi}{3}\right)+3\in\left[1;5\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=1\\y_{max}=5\end{matrix}\right.\)
E
0
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(y=2-2.\left(2sinx.cosx\right)=2-2sin2x\)
Do \(-1\le sin2x\le1\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(sin2x=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
\(y_{max}=4\) khi \(sin2x=-1\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
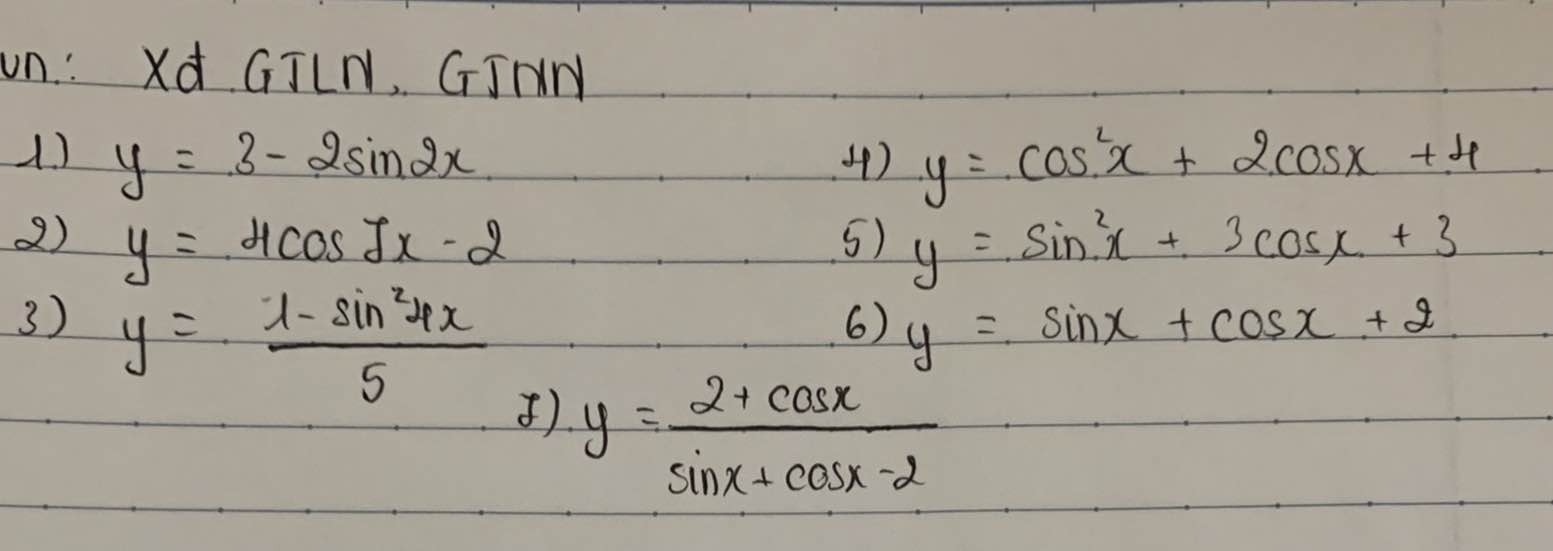
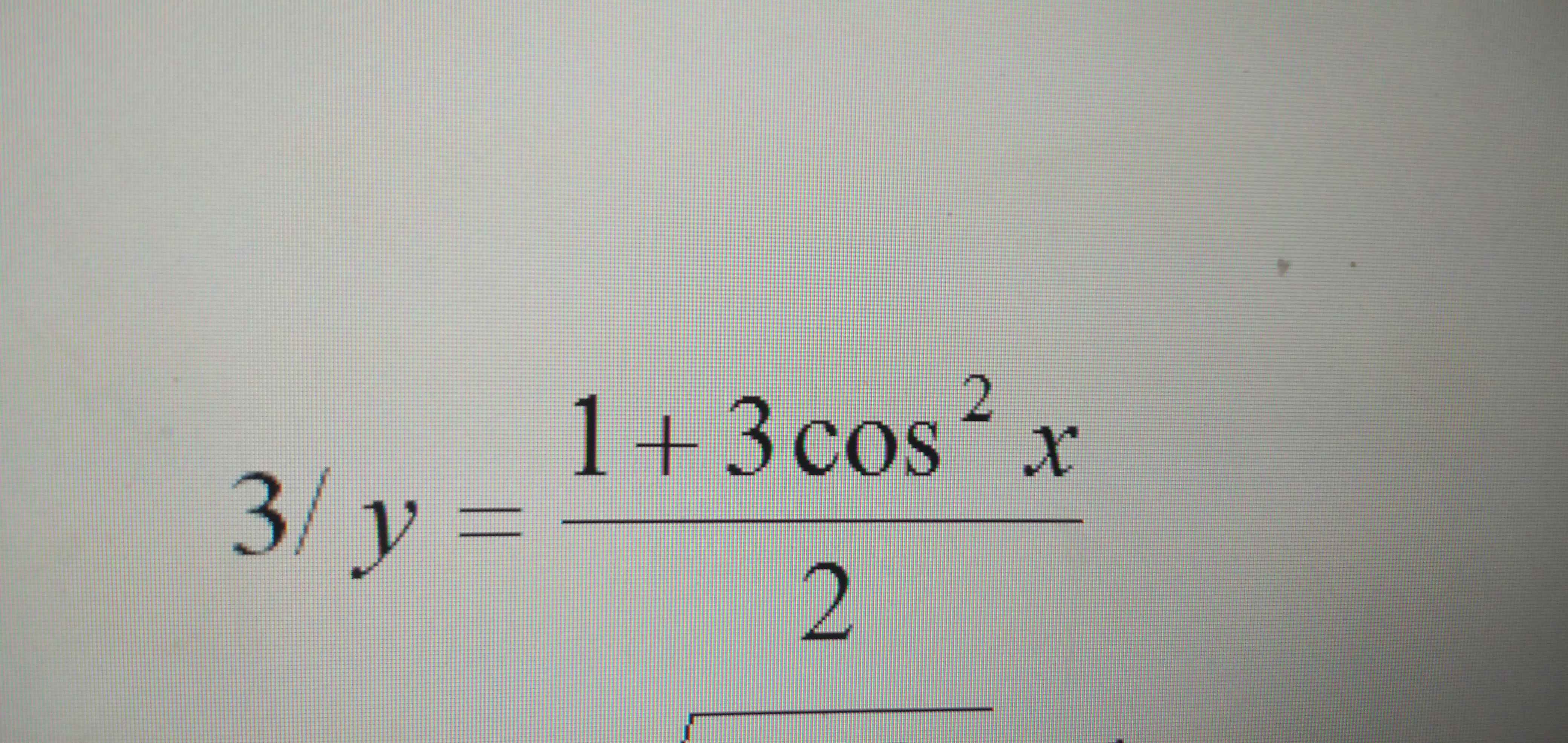
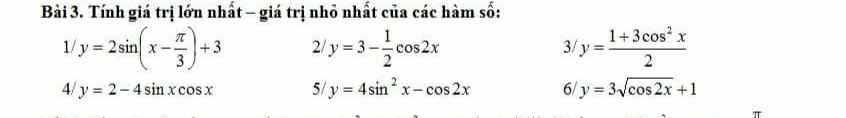
ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)
Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)