K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
2
9 tháng 3 2023
\(\text{#TNam}\)
`5,A`
Gọi các cạnh của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
`3` góc của tam giác lần lượt tỉ lệ với `2:3:4`
Nghĩa là: `x/2=y/3=z/4`
Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=`\(\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=20\\\dfrac{y}{3}=20\\\dfrac{z}{4}=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=20\cdot2=40\\y=20\cdot3=60\\z=20\cdot4=80\end{matrix}\right.\)
Vậy, độ dài các cạnh của Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0`.
`6,B`
Gọi số người thợ của `3` nhóm lần lượt là `x,y,z (x,y,z \ne 0)`
Vì năng suất làm việc của các người thợ như nhau `->` số thợ và số ngày là `2` đại lượng tỉ lệ nghịch
`-> 40x=60y=50z` hay \(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}=\dfrac{x-z}{\dfrac{1}{40}-\dfrac{1}{50}}=\dfrac{3}{\dfrac{1}{200}}=600\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{40}}=600\\\dfrac{y}{\dfrac{1}{60}}=600\\\dfrac{z}{\dfrac{1}{50}}=600\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=600\cdot\dfrac{1}{40}=15\\y=600\cdot\dfrac{1}{60}=10\\z=600\cdot\dfrac{1}{50}=12\end{matrix}\right.\)
Vậy, số thợ của nhóm `1,2,3` lần lượt là `15,10,12`.
31 tháng 3 2016
Xét tam giác ABD và tam giác ACDcó AB+BD>AD vàAC+CD>AD(BĐT tam giác ABD và ACD)
Cộng 2 vế lại với nhau ta được:
AB+AC+BD+CD>2AD
=>AB+AC+BC>2AD
Mà AB+AC+BC là chu vi của tam giác ABC
=>1/2(AB+AC+BC)>AD
Vậy nửa chu vi của tam giác ABC>AD
31 tháng 10 2021
14: \(=\dfrac{1}{9}+\dfrac{10}{9}+2:\dfrac{9}{7}=\dfrac{11}{9}+\dfrac{14}{9}=\dfrac{25}{9}\)
15: \(=\dfrac{3^4\cdot3^3}{3^7}\cdot2018=2018\)
12 tháng 3 2022
a: \(\widehat{B}=\dfrac{180^0-80^0}{2}=50^0\)
b: Chiều dài là \(\sqrt{15^2-9^2}=12\left(dm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 12 2021
\(\dfrac{\sqrt{5^2}-\sqrt{19^2}}{\sqrt{8^2}-\sqrt{22^2}}=\dfrac{5-19}{8-22}=\dfrac{-14}{-14}=1\)
D
13 tháng 4 2017
N=7.(2007^2009-2013^1999)/10 (1)
{Để chứng minh N nguyên thì cần c/m:2007^2009-2013^1999 chia hết cho 10}
Ta có:
*2007^2009
=2007.(2007^4)^502
=2007.(...1)^502
=2007.(...1)=(...7)
*2013^1999
=2013^3.(2013^4)^499
=(...7).(...1)^499
=(...7).(...1)=(...7)
=>2007^2009-2013^1999
=(..7)-(...7)=(...0)
nên chia hết cho 10 (2)
Từ (1),(2)=>N thuộc Z và N là hợp số vì N chia hết cho 7
3 tháng 8 2017
Theo đề bài, ta có:
\(\frac{2}{3}x^2-2=\frac{2}{3}\)
\(\frac{2}{3}x^2=\frac{2}{3}+2\)
\(\frac{2}{3}x^2=\frac{8}{3}\)
\(x^2=\frac{8}{3}\div\frac{2}{3}\)
\(x^2=4\)
\(x=\text{±}2\)
2P
1
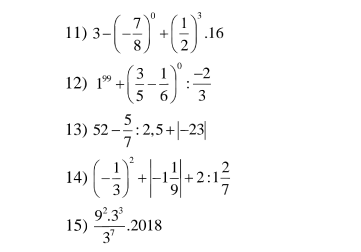
Chọn A
Đáp án A nha bạn