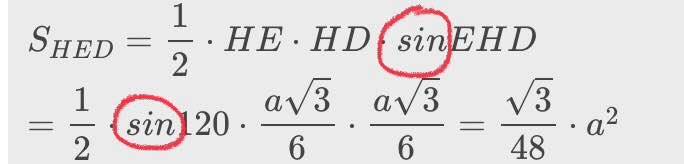Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB và AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
=>góc ABC=góc ADE
b: Xét ΔHEB vuông tại E và ΔHDC vuôg tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HD*HB và HE/HB=HD/HC
=>ΔHED đồng dạng với ΔHBC
d: ΔABC đều
=>H là trọng tâm
=>HD=1/3BD=\(\dfrac{1}{3}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\) và \(HE=\dfrac{1}{3}CE=\dfrac{a\sqrt{3}}{6}\)
\(S_{HED}=\dfrac{1}{2}\cdot HE\cdot HD\cdot sinEHD\)
\(=\dfrac{1}{2}\cdot sin120\cdot\dfrac{a\sqrt{3}}{6}\cdot\dfrac{a\sqrt{3}}{6}=\dfrac{\sqrt{3}}{48}\cdot a^2\)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(\dfrac{S_{HED}}{S_{BAC}}=\dfrac{\sqrt{3}}{48}:\dfrac{\sqrt{3}}{4}=\dfrac{1}{12}\)

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: \(AM=\dfrac{AB}{2}\)
\(AN=\dfrac{AC}{2}\)
\(MN=\dfrac{BC}{2}\)
mà AB=AC=BC
nên AM=MN=AN
hay ΔAMN đều

a: \(A=\dfrac{x\left(x+2\right)}{\left(x-2\right)^2}:\dfrac{x^2-4+x+6-x^2}{x\left(x-2\right)}\)
\(=\dfrac{x\left(x+2\right)}{x-2}\cdot\dfrac{x}{x+2}=\dfrac{x^2}{x-2}\)
c: A<0
=>x-2<0
=>x<2
d: B nguyên
=>x^2-4+4 chia hết cho x-2
=>x-2 thuộc {1;-1;2;-2;4;-4}
=>x thuộc {3;1;4;6}

Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)

c: Gọi bốn số nguyên liên tiếp là x;x+1;x+2;x+3
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1\)
\(=\left(x^2+3x+1\right)^2\)
\(d,M=\left(x^2-4xy+4y^2\right)-2\left(x-2y\right)+1+9\\ M=\left(x-2y\right)^2-2\left(x-2y\right)+1+9\\ M=\left(x-2y+1\right)^2+9\ge9\\ M_{min}=9\Leftrightarrow x=2y-1\)

c: \(2x^3-50x=0\)
\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)

c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)

Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{72}{x+3}+\dfrac{54}{x-3}=6\Rightarrow x=21\left(tm\right)\)




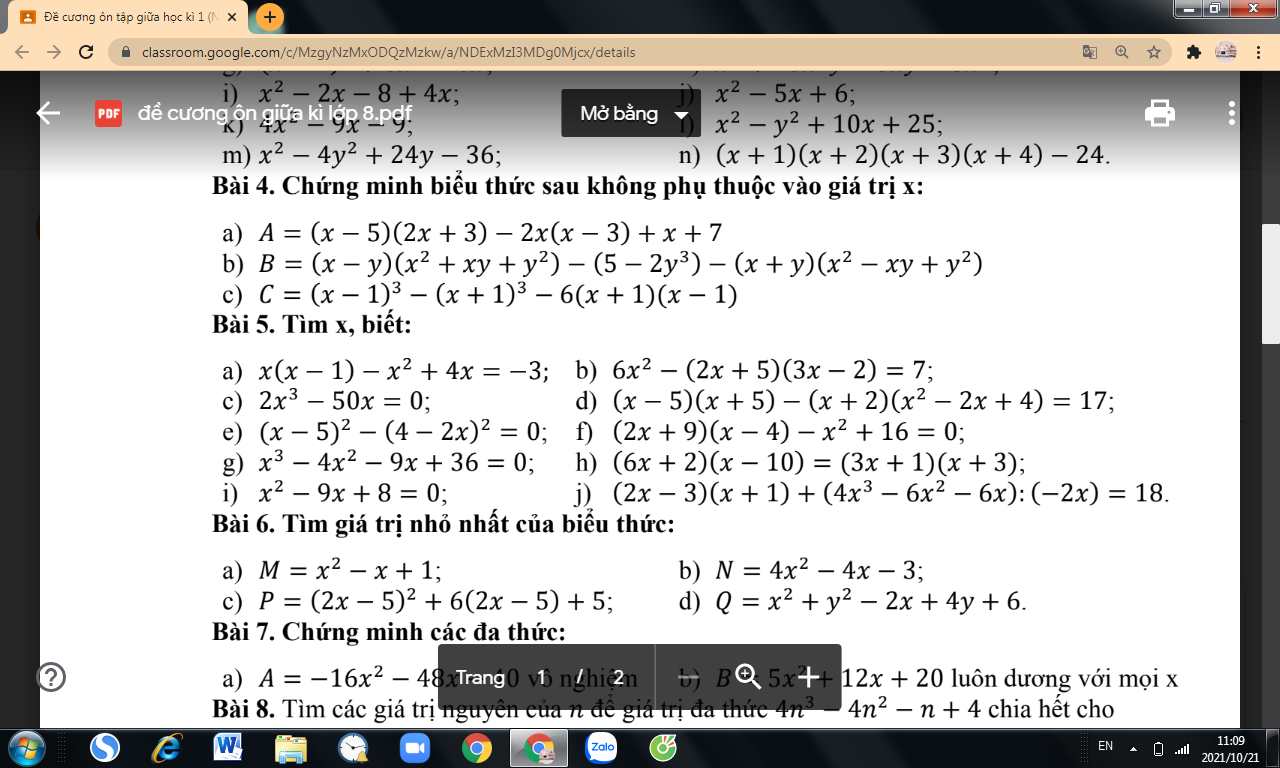
 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ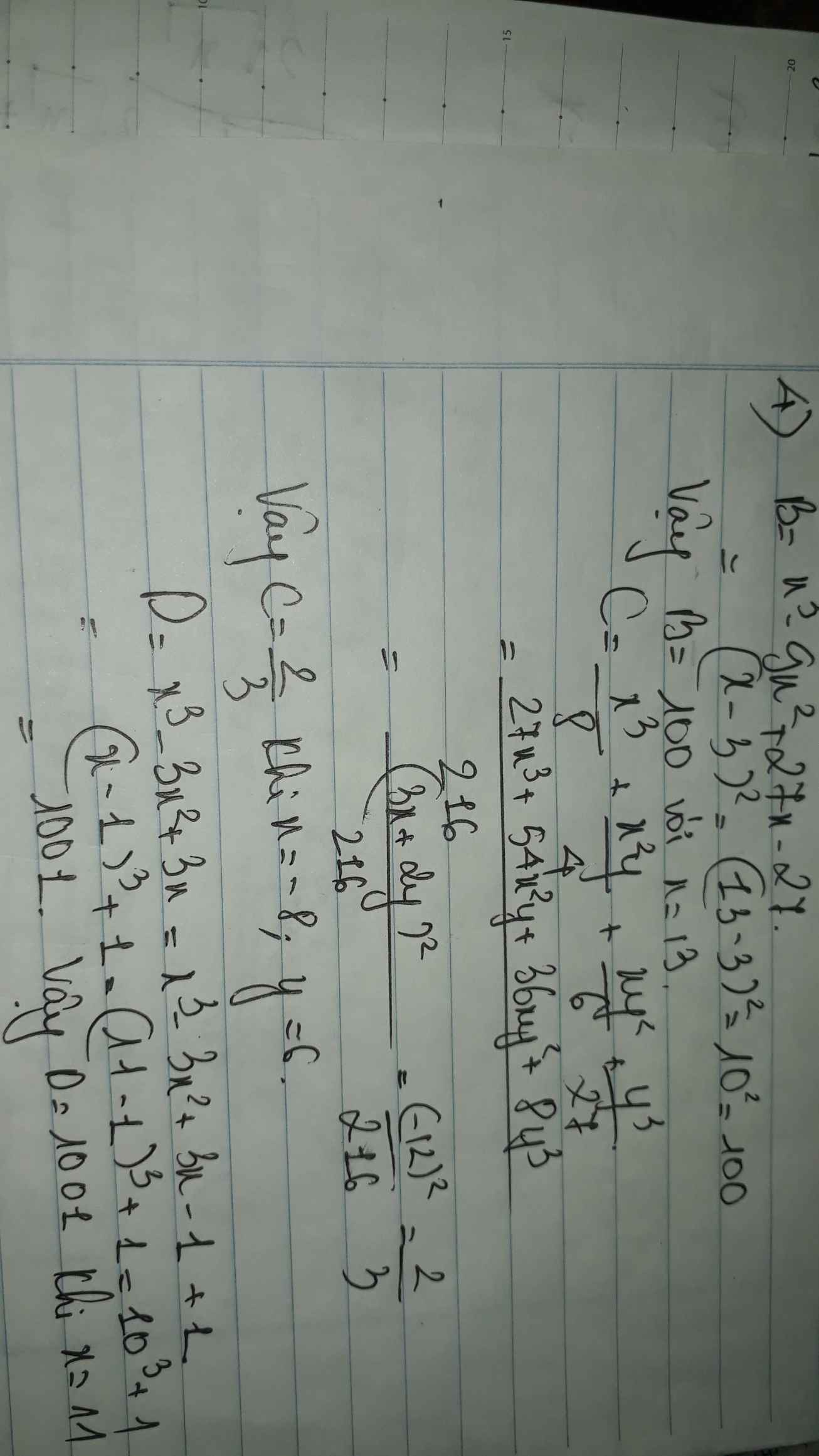

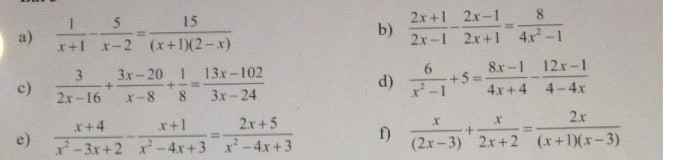

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB và AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
=>góc ABC=góc ADE
b: Xét ΔHEB vuông tại E và ΔHDC vuôg tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HD*HB và HE/HB=HD/HC
=>ΔHED đồng dạng với ΔHBC
d: ΔABC đều
=>H là trọng tâm
=>HD=1/3BD=\(\dfrac{1}{3}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\) và \(HE=\dfrac{1}{3}CE=\dfrac{a\sqrt{3}}{6}\)
\(S_{HED}=\dfrac{1}{2}\cdot HE\cdot HD\cdot sinEHD\)
\(=\dfrac{1}{2}\cdot sin120\cdot\dfrac{a\sqrt{3}}{6}\cdot\dfrac{a\sqrt{3}}{6}=\dfrac{\sqrt{3}}{48}\cdot a^2\)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(\dfrac{S_{HED}}{S_{BAC}}=\dfrac{\sqrt{3}}{48}:\dfrac{\sqrt{3}}{4}=\dfrac{1}{12}\)
Cậu giải thích cho mình này nghĩa là gì được không, mình không biết