
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: ĐKXĐ: y>=-1
Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
2a+b=0 và 3a-2b=-7
=>4a+2b=0 và 3a-2b=-7
=>a=-1 và b=2
=>x=-1 và y+1=4
=>x=-1 và y=3
c: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
a+3b=1 và 2a-3b=2
=>3a=3 và a+3b=1
=>a=1 và b=0
=>x-1=1 và y-2=0
=>x=2 và y=2
d: ĐKXĐ: x<>0 và y>=-3
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
4a-b=2 và a+b=3
=>5a=5 và a+b=3
=>a=1 và b=2
=>x=1 và y+3=4
=>x=1 và y=1

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)



Bài 3:
\(a,m=-2\Leftrightarrow y=-3x-3\\ b,\Leftrightarrow\left\{{}\begin{matrix}m-1=2\\2m+1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne0\end{matrix}\right.\Leftrightarrow m=3\\ c,\text{PT hoành độ giao điểm: }2x-7=\left(m-1\right)x+2m+1\\ \text{Thay }x=2\\ \Leftrightarrow2m-2+2m+1=-3\\ \Leftrightarrow4m=-2\Leftrightarrow m=-\dfrac{1}{2}\\ d,\text{Gọi điểm cần tìm là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=\left(m-1\right)x_0+2m+1\\ \Leftrightarrow mx_0-x_0+2m+1-y_0=0\\ \Leftrightarrow m\left(x_0+2\right)+\left(1-x_0-y_0\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0+2=0\\1-x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-2\\y_0=3\end{matrix}\right.\Leftrightarrow A\left(-2;3\right)\)


2: FK vuôg góc BE; AE vuông góc BE
=>FK//AE
Chứng minh tương tự, ta được AF//EK
=>AFKE là hbh
=>AF=EK
=>AF/EC=EK/EC
ΔCEK đồng dạng với ΔCAM
=>EK/EC=AM/AC
=>AF/EC=AM/AC
ΔAFB đồng dạng với ΔCEB
=>góc ABF=góc CBE
c: AM/AC=AF/EC=AB/BC
=>AM/AC=AB/BC
=>ΔAMB đồng dạng với ΔCAB
=>góc ABC=góc ABM
=>BA là phân giác của góc MBC


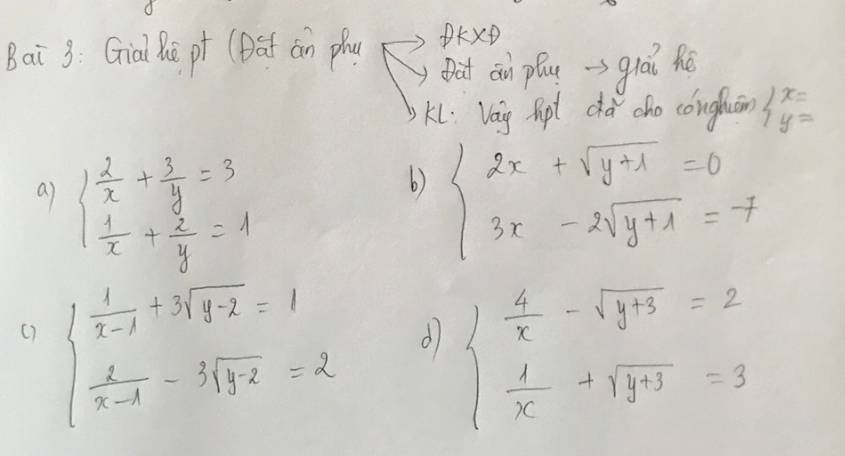
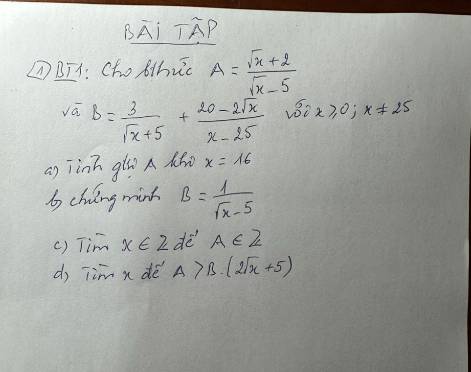

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 


