
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3

d: Xét ΔABK và ΔCKB có
AB=CK
KB chung
AK=CB
Do đó: ΔABK=ΔCKB

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC

5:
=10x^3*1/2xy-2/5y*1/2xy+1/2z*1/2xy
=5x^3y-1/5xy^2+1/4xyz
6: =x^2y*4xy+x^2y*3y-5x*x^2y
=4x^3y^2+3x^2y^2-5x^3y
7: =-4/3xy*3x^2y+4/3xy*6xy-4/3xy*9x
=-4x^3y^2+8x^2y^2-12x^2y

\(-x-\dfrac{3}{5}=-\dfrac{6}{7}\)
\(\Rightarrow-\left(x+\dfrac{3}{5}\right)=-\dfrac{6}{7}\)
\(\Rightarrow x+\dfrac{3}{5}=\dfrac{6}{7}\)
\(\Rightarrow x=\dfrac{6}{7}-\dfrac{3}{5}\)
\(\Rightarrow x=\dfrac{9}{35}\)

b,Vì:2x=3y
=>x=3y:2(1)
Vì:xy=54(2)
Thay(1) vào (2), ta có:
3y:2.y=54
3y.y=54.2
3.y2=108
y2=108:3
y2=36
y^2=6^2 hoặc y^2=(-6)^2
y=6 hoặc y=-6
Song bạn thay vào (1) hoặc (2) để tìm x nhé!!
Bạn nhớ k cho mình nha!!
2x=3y suy ra x/3=y/2
đặt x/3=y/2=k suy ra x =3k, y=2k
xy =3k x 2k =5 4
xy =6 x k^2 = 54
suy ra k^2 = 9
suy ra k bằng 3 hoặc -3 suy ra x=9 hoặc -9 , ý= -6 hoặc 6


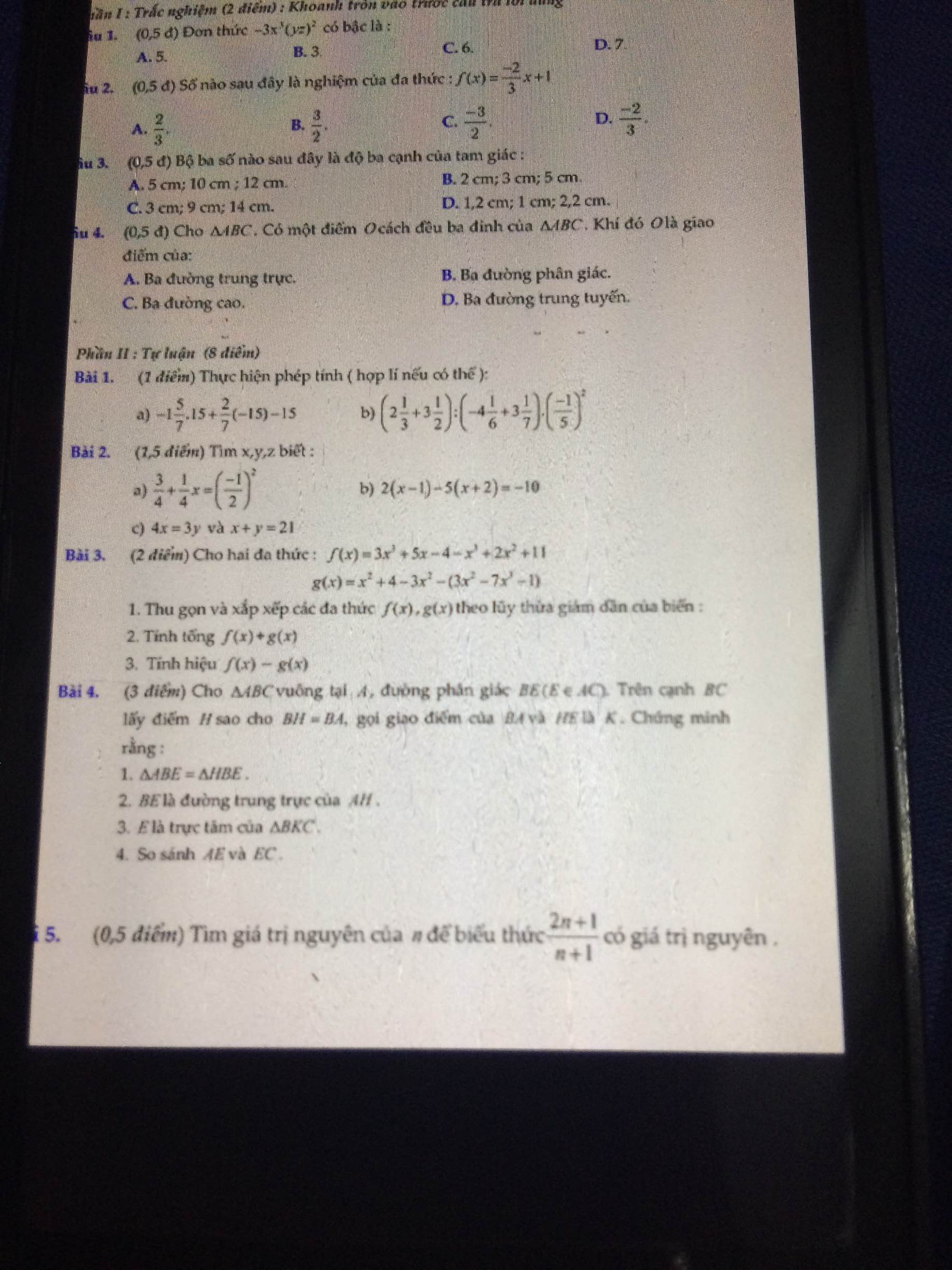
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔCDA và ΔABC có
AD=CB
\(\widehat{DAC}=\widehat{BCA}\)(hai góc so le trong, DA//BC)
CA chung
Do đó: ΔCDA=ΔABC

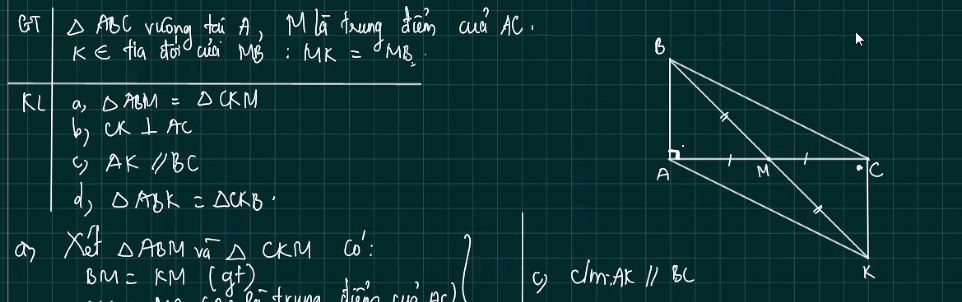 giúp mình câu d với
giúp mình câu d với 



6.
a) \(\left|x-\frac{1}{2}\right|\le\frac{1}{3}\)\(\Rightarrow\left|x-\frac{1}{2}\right|\le\left|\frac{1}{3}\right|\)
\(\Rightarrow\frac{-1}{3}\le x-\frac{1}{2}\le\frac{1}{3}\)
\(\Rightarrow\frac{1}{6}\le x\le\frac{5}{6}\)
b) \(\left|2x-\frac{1}{2}\right|>\left|-1,5\right|\)
\(\Rightarrow\orbr{\begin{cases}-1,5< 2x-\frac{1}{2}< 1,5\\2x-\frac{1}{2}< -1,5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\frac{-3}{2}< 2x-\frac{1}{2}< \frac{3}{2}\\2x-\frac{1}{2}< \frac{-3}{2}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\frac{-3}{2}< 2x-\frac{1}{2}< \frac{3}{2}\\2x-\frac{1}{2}< \frac{-3}{2}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}-1< 2x< 2\\2x< -1\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}\frac{-1}{2}< x< 1\\x< \frac{-1}{2}\end{cases}}\)
7.
a) \(\left|-2x+1,5\right|=\frac{1}{4}\)
\(\Rightarrow\orbr{\begin{cases}-2x+\frac{3}{2}=\frac{1}{4}\\-2x+\frac{3}{2}=\frac{-1}{4}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}-2x=\frac{7}{4}\\-2x=\frac{5}{4}\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=\frac{-7}{8}\\x=\frac{-5}{8}\end{cases}}\)
b) \(\frac{3}{2}-\left|1\frac{1}{4}+3x\right|=\frac{1}{4}\)
\(\Rightarrow\left|\frac{5}{4}+3x\right|=\frac{3}{2}-\frac{1}{4}=\frac{5}{4}\)
\(\Rightarrow\orbr{\begin{cases}\frac{5}{4}+3x=\frac{5}{4}\\\frac{5}{4}+3x=\frac{-5}{4}\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}3x=0\\3x=\frac{-5}{2}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{-5}{6}\end{cases}}\)