
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(\frac{5}{1\cdot7}+\frac{5}{7\cdot13}+\frac{5}{13\cdot19}+...+\frac{5}{91\cdot97}\)
= \(5\cdot\frac{1}{6}\cdot\left(\frac{6}{1\cdot7}+\frac{6}{7\cdot13}+\frac{6}{13\cdot19}+...+\frac{6}{91\cdot97}\right)\)
= \(\frac{5}{6}\cdot\left(1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+\frac{1}{13}-\frac{1}{19}+...+\frac{1}{91}-\frac{1}{97}\right)\)
= \(\frac{5}{6}\cdot\left(1-\frac{1}{97}\right)\)
= \(\frac{5}{6}\cdot\frac{96}{97}\)
= \(\frac{80}{97}\)
5/1.7 + 5/7.13 + 5/13.19 + ... + 5/91.97
= 5/6.(1 - 1/7 + 1/7 - 1/13 + 1/13 - 1/19 + ... + 1/91 - 1/97)
= 5/6.(1 - 1/97)
= 5/6.96/97
= 80/97

\(\frac{5x+7}{4}+\frac{3x+5}{8}>\frac{9x+4}{5}\)
\(\frac{10\cdot\left(5x+7\right)}{40}+\frac{5\cdot\left(3x+5\right)}{40}>\frac{8\cdot\left(9x+4\right)}{40}\)
10.(5x + 7) + 5.(3x + 5) > 8.(9x + 4)
10.(5x + 7) + 5.(3x + 5) - 8.(9x + 4) > 0
50x + 70 + 15x + 25 - 72x - 32 > 0
- 7x + 63 > 0
- 7.(x - 9) > 0
\(\Rightarrow x-9


\(\frac{x}{5}=\frac{y}{3}\)và x2-y2=4(x,y>0)
\(\Rightarrow\frac{x}{5}=\frac{y}{3}=\frac{x^2}{5^2}=\frac{y^2}{3^2}=\frac{x^2-y^2}{25-9}=\frac{4}{16}=\frac{1}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\Rightarrow\frac{x^2}{25}=\frac{1}{4}\Rightarrow x^2=\frac{25}{4}\Rightarrow x=\frac{5}{2}\)
\(\Rightarrow\frac{y^2}{9}=\frac{1}{4}\Rightarrow y^2=\frac{9}{4}\Rightarrow y=\frac{3}{2}\)
Vậy x =\(\frac{5}{2}\)và y =\(\frac{3}{2}\)
Ta có:
\(\frac{x}{3}=\frac{y}{5}\Rightarrow\frac{x^2}{3}=\frac{y^2}{5}\)
Áp dụng dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{3^2}=\frac{y^2}{5^2}=\frac{x^2-y^2}{3^2-5^2}=\frac{-4}{-16}=\frac{1}{4}\)
\(\Rightarrow\frac{x^2}{3^2}=\frac{1}{4}\Rightarrow x=\sqrt{3^2.\frac{1}{4}}=\frac{3}{2}\)
\(\frac{y^2}{5^2}=\frac{1}{4}\Rightarrow y=\sqrt{5^2.\frac{1}{4}}=\frac{5}{2}\)


Bài 4:
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD

Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)


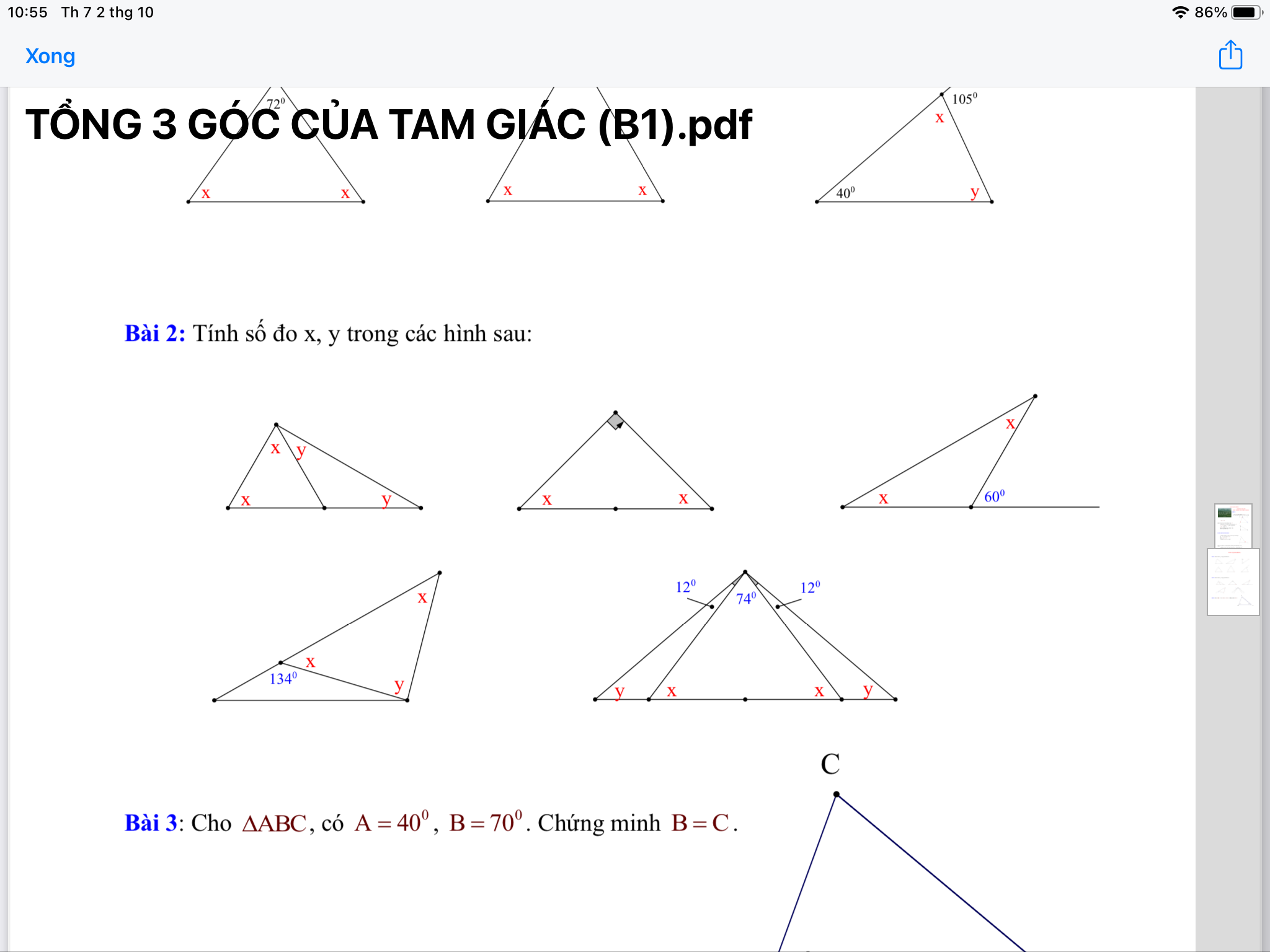
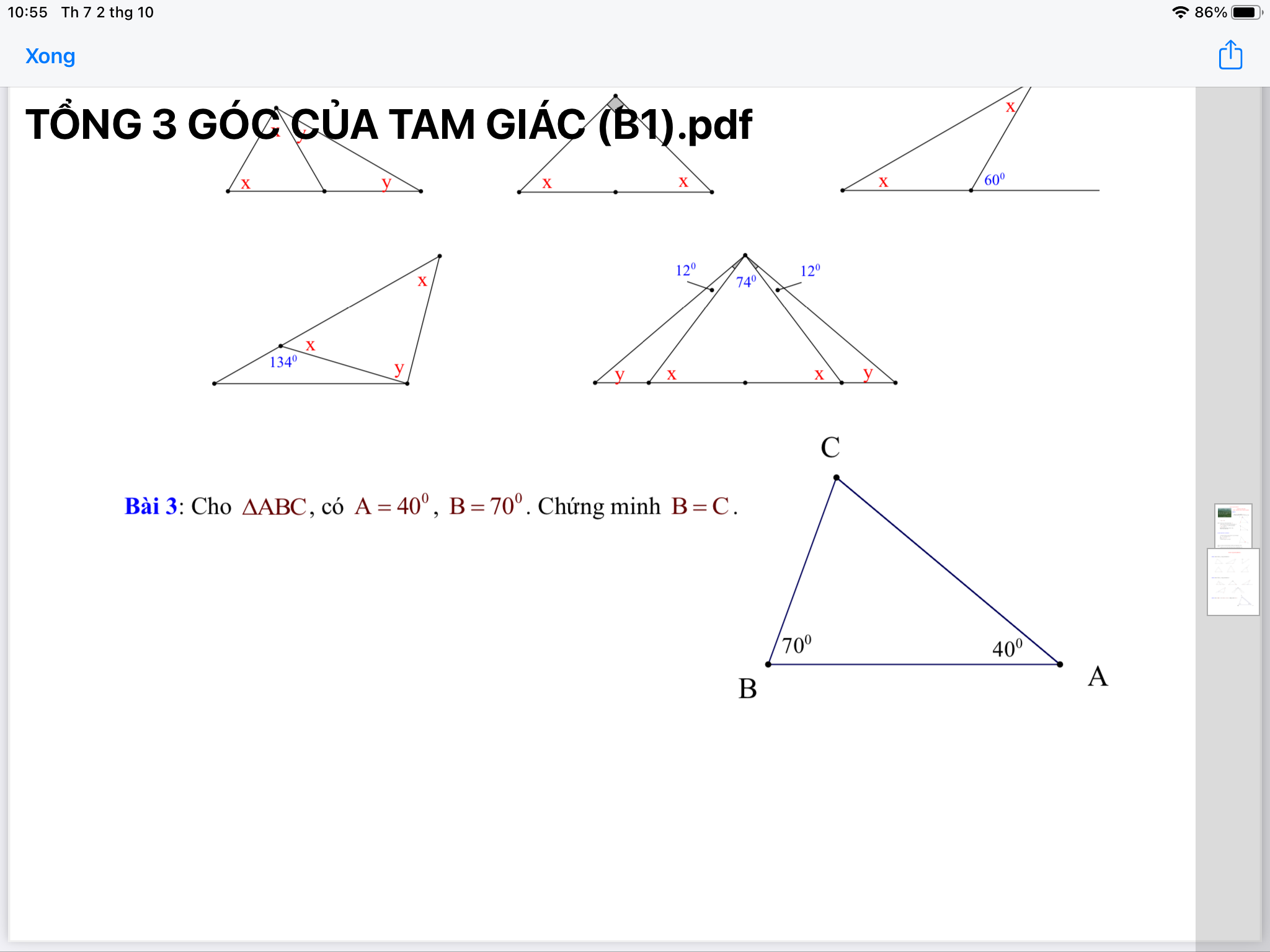




Mình chỉ thấy rõ đề mấy câu này thôi, những câu còn lại bạn chụp mờ quá nên không thấy rõ. Bạn nên chụp lại cho rõ hơn nhé.