K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 2 2022
Bài 4:
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{KAC}\) chung
Do đó:ΔABH=ΔACK
Suy ra: BH=CK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{OCB}=\widehat{OBC}\)
hay ΔOBC cân tại O
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
Suy ra: \(\widehat{BAO}=\widehat{CAO}\)
hay AO là tia phân giác của góc BAC
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
23 tháng 2 2022
Bài 4:
a: Xét tứ giác ABEC có
M là trung điểm của AC
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//CE và AB=CE
c: Xét tứ giác APEQ có
AP//EQ
AP=EQ
Do đó: APEQ là hình bình hành
Suy ra: Hai đường chéo AE và PQ cắt nhau tại trung điểm của mỗi đường
mà M là trug điểm của AE
nên M là trung điểm của PQ
N
5
TA
1
10 tháng 5 2022
a, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=10^2+8^2\)
=> \(BC^2=164\)
=> \(BC=12,8\left(cm\right)\)
b, Xét Δ ABE và Δ HBE, có :
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác \(\widehat{ABC}\))
\(\widehat{BAE}=\widehat{BHE}=90^o\)
BE là cạnh chung
=> Δ ABE = Δ HBE (g.c.g)
=> AB = HB
Xét Δ ABH, có : AB = HB (cmt)
=> Δ ABH cân tại B
c,
Gọi O là giao điểm của tia AH và BE
Xét Δ cân ABH, có :
BO là tia phân giác \(\widehat{ABH}\)
=> BO là đường cao
=> \(BO\perp AH\)
=> \(BE\perp AH\)
30 tháng 4 2022
Bài 6:
a: Đặt 4x-1/2=0
=>4x=1/2
hay x=1/8
b: Đặt (x-1)(x+1)=0
=>x-1=0 hoặc x+1=0
=>x=1 hoặc x=-1
28 tháng 8 2016
\(\left|x-\frac{1}{3}+\frac{4}{5}\right|=\left|-3,2+\frac{2}{5}\right|\)
\(\Rightarrow x-\frac{1}{3}+\frac{4}{5}=-3,2+\frac{2}{5}\)
\(\Rightarrow x-\frac{1}{3}+\frac{4}{5}=-\frac{14}{5}\)
\(\Rightarrow x-\frac{1}{3}=-\frac{14}{5}-\frac{4}{5}\)
\(\Rightarrow x-\frac{1}{3}=-\frac{18}{5}\)
\(\Rightarrow x=\frac{-49}{15}\)
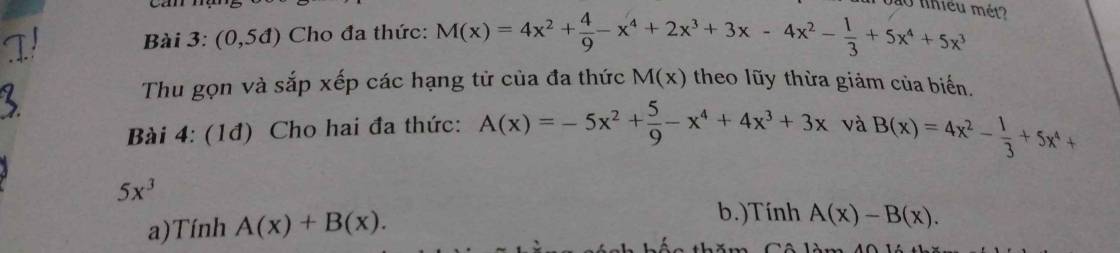
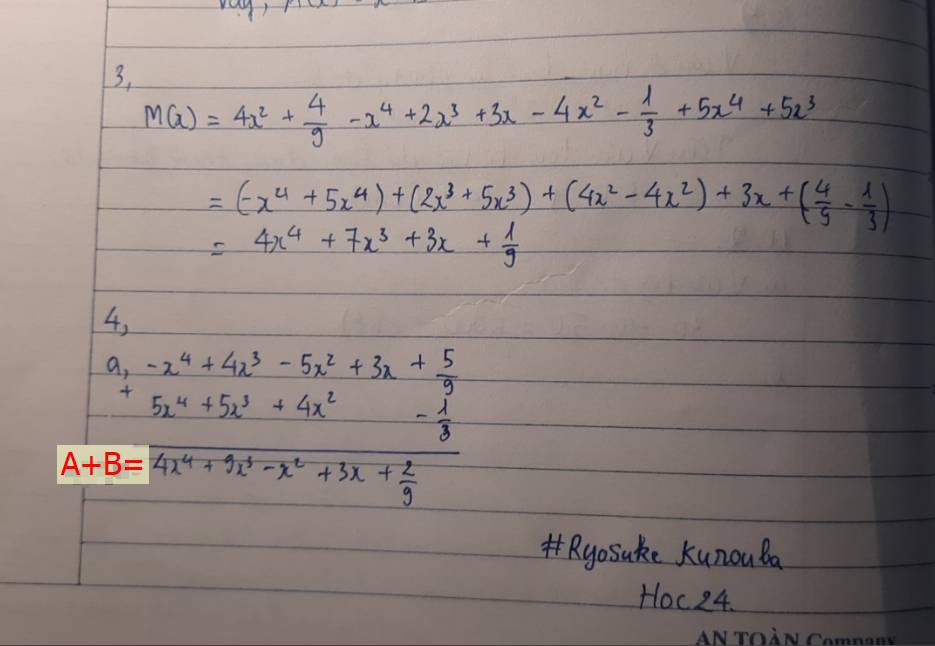
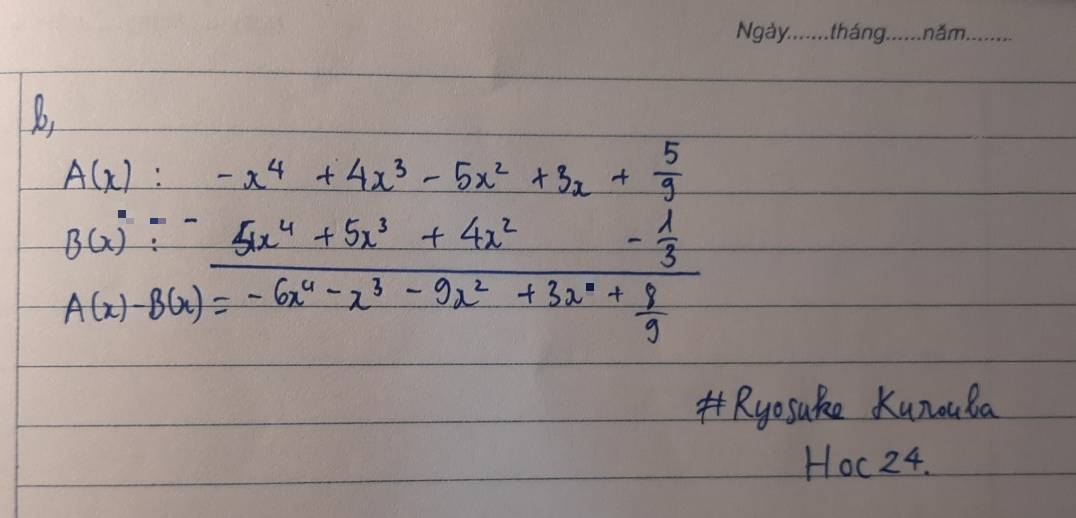
Ta có: \(\widehat{xOn}=\widehat{xOy}-\widehat{yOn}\)
\(\widehat{yOm}=\widehat{xOy}-\widehat{mOx}\)
Mà : \(\widehat{yOn}=\widehat{mOx}=90^o\)
\(\widehat{xOy}\) chung
=> \(\widehat{xOn}=\widehat{mOy}\)
b)Ta có: \(\widehat{yOn}+\widehat{mOx}=90^o+90^o\)
\(\widehat{yOn}+\widehat{mOx}=180^o\)
mà \(\widehat{xOm}=\widehat{xOn}+\widehat{nOm}\)
\(\widehat{yOn}=\widehat{yOm}+\widehat{nOm}\)
=>\(\widehat{yOm}+\widehat{nOm}+\widehat{xOn}+\widehat{nOm}=180^o\)
Ta thấy \(\widehat{xOy}=\widehat{xOn}+\widehat{nOm}+\widehat{yOm}\)
=> \(\widehat{xOy}+\widehat{nOm}=180^o\)