giúp mình 3 bài trên với ạ! mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2H
giúp mình với ạ,mình xin cảm ơn trước
1
21 tháng 11 2021
Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs
3N
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
1
12 tháng 2 2022
=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ
NA
1
12 tháng 12 2023
Bài 3:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét tứ giác ABCI có
AI//BC
AI=BC
Do đó: ABCI là hình bình hành
=>AB//CI
Ta có: AB//CI
AB//CD
CD,CI có điểm chung là C
Do đó: D,C,I thẳng hàng
Bài 4:
a: Ta có: AB là đường trung trực của ME
=>AM=AE; BM=BE
Ta có: AC là đường trung trực của MF
=>AM=AF và CM=CF
Ta có: AM=AE
AM=AF
Do đó: AE=AF
=>A nằm trên đường trung trực của EF
b: BE+CF
=BM+CM
=BC
c: Xét ΔAEB và ΔAMB có
AE=AM
EB=MB
AB chung
Do đó: ΔABE=ΔABM
=>\(\widehat{EAB}=\widehat{MAB}\)
mà tia AB nằm giữa hai tia AE,AM
nên AB là phân giác của góc EAM
=>\(\widehat{EAM}=2\cdot\widehat{BAM}\)
Xét ΔAMC và ΔAFC có
AM=AF
CM=CF
AC chung
Do đó: ΔAMC=ΔAFC
=>\(\widehat{MAC}=\widehat{FAC}\)
mà tia AC nằm giữa hai tia AM,AF
nên AC là phân giác của góc MAF
=>\(\widehat{MAF}=2\cdot\widehat{MAC}\)
Ta có: \(\widehat{EAF}=\widehat{EAM}+\widehat{FAM}\)
\(=2\cdot\widehat{MAB}+2\cdot\widehat{MAC}\)
\(=2\left(\widehat{MAB}+\widehat{MAC}\right)=2\cdot\widehat{BAC}=120^0\)
Xét ΔAEF có AE=AF
nên ΔAEF cân tại A
=>\(\widehat{AEF}=\widehat{AFE}\)(2)
=>\(\widehat{AEF}=\widehat{AFE}=\dfrac{180^0-120^0}{2}=30^0\)
d: Xét ΔAEI và ΔAMI có
AE=AM
\(\widehat{EAI}=\widehat{MAI}\)
AI chung
Do đó: ΔAEI=ΔAMI
=>\(\widehat{AEI}=\widehat{AMI}\)(1)
Xét ΔAMK và ΔAFK có
Am=AF
\(\widehat{MAK}=\widehat{FAK}\)
AK chung
Do đó: ΔAMK=ΔAFK
=>\(\widehat{AMK}=\widehat{AFK}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{AMI}=\widehat{AMK}\)
=>MA là phân giác của góc IMK
e: Để A là trung điểm của EF thì \(\widehat{EAF}=180^0\)
=>\(\widehat{BAC}=\dfrac{\widehat{EAF}}{2}=\dfrac{180^0}{2}=90^0\)
ND
0
HN
3
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)
YN
2
H
28 tháng 4 2022
1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM
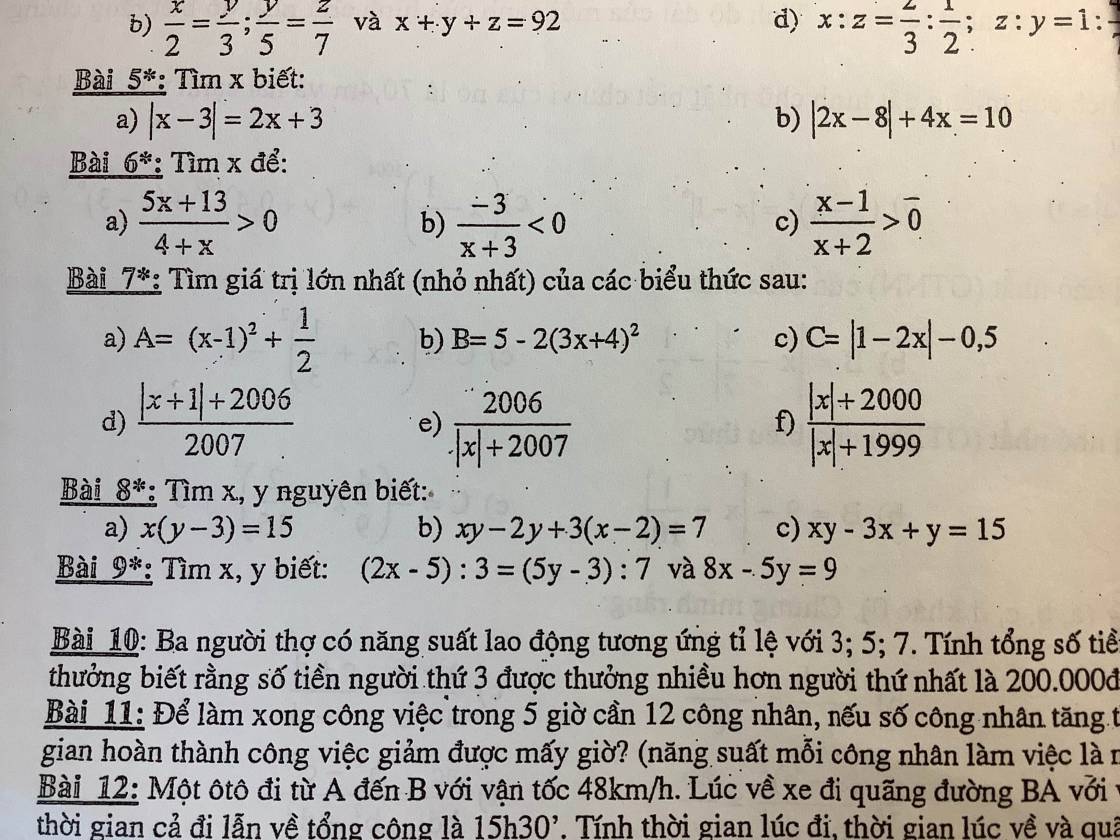
12: Gọi vận tốc lúc về là x
Theo đề, ta có: x/60=1:0,8=5/4
=>x=75
11:
b: k=xy=4,5
Khi y=-0,5 thì x=4,5/-0,5=-9
c: v2*t2=v1*t1
=>t2/t1=v1/v2=5/6
d: Chiều dài và chiều rộng là hai đại lượng tỉ lệ nghịch
=>Nếu tăng chiều dài lên a lần và muốn giữ nguyên diện tích thì cần giảm chiều rộng đi a lần